Introduction to statistics

Even if you aren’t going to be doing any statistical analysis yourself, being able to interpret and critically evaluate published statistics will enable you to get the most out of the journal articles and other literature you read. This page details some commonly reported statistics and how to interpret them (although note that if you are looking to gain a more fundamental understanding of of how to interpret a few common graphs and tables and calculate a few key values, you may find that the statistics section of the Statistics and probability page of the Numeracy fundamentals module is more suitable instead).

Interpreting descriptive statistics

Descriptive statistics are used to summarise and describe the data you have access to, be it:

• data for the whole population of interest (such as everyone who attends a particular school), or
• data collected from a random sample of a larger population (such as a random sample of people who were patients at a particular hospital over a two year period).

The only difference is that in the latter situation, which occurs most often, descriptive statistics do not allow any conclusions to be drawn about the wider population, so will typically be used in conjunction with other statistics. More on these shortly, but for now let’s consider the descriptive statistics in Table 1.

Table 1
Participant Characteristics

From “Examining Associations between Health, Wellbeing and Social Capital: Findings from a Survey Developed and Conducted using Participatory Action Research,” by S. Visram, S. Smith, N. Connor, G. Greig, & C. Scorer, 2018, Journal of Public Mental Health , 17 (3), p. 127 (https://doi.org/10.1108/JPMH-09-2017-0035). Copyright 2018 by Emerald Publishing Limited.

This data was obtained from a sample of people who live in a particular city, and the sample size is \(233\) (as indicated by the \(n = 233\) at the bottom of the table). Moreover, there are two different types of variables summarised in this table:

1. categorical variables, for data grouped into categories (the ‘Gender’ variable for example), and
2. continuous variables, for numerical data (the ‘Age in years’ variable for example).

These two types of variables need to, and have been, analysed differently.

Let’s look at the categorical variables first (alternatively, if you would like more information on the different types of variables please refer to the Data and variable types page of this module).

Interpreting descriptive statistics for categorical variables

The categorical variables in this example have been summarised using percentages, and these show what percentage of the sample is in each category for the given variable (note that frequencies are sometimes used instead of percentages, and that these show how many are in each category instead). For example, the descriptive statistics for the ‘Gender’ variable show that \(65.7\%\) of the sample described in Table 1 are women and \(34.3\%\) are men.

If you would like to learn more about descriptive statistics for categorical variables, including how to calculate them, please refer to the Descriptive statistics for one categorical variable section of this module. Otherwise, to practise interpreting descriptive statistics for categorical variables have a go at the following question.

Interpreting descriptive statistics for continuous variables

The continuous variables in this example have been summarised using two measures, the first being the mean (also called the arithmetic average). This is the most commonly used measure of central tendency, and is a single value used to describe the data set by indicating the central value. For example, in Table 1 the mean for the ‘Age in years’ variable is \(47.3\), indicating that the average (or central) age of the sample of \(233\) people is \(47.3\). The second measure is the standard deviation (SD), which is the most commonly used measure of dispersion. This is a single value used to describe the data set by indicating how varied (or spread out) it is. The standard deviation for the ‘Age in years’ variable in Table 1 is \(17.4\). This is quite large relative to the mean, indicating that the variability in the ages of the sample of \(233\) people is quite large.

Summarising continuous variables using both a measure of central tendency and a measure of dispersion in this way is optimal, as one without the other does not fully describe the variable. For example, if we were only provided with \(47.3\) as the mean age of the sample then we would have no way of knowing whether everyone in the sample was \(47.3\), or whether the ages of the people in the sample were widely dispersed either side of \(47.3\). Likewise, if we were only provided with the standard deviation of \(17.4\) then we would have no way of knowing the central value of the data set.

It is important to note that the mean and standard deviation are not the only measures of central tendency and dispersion respectively though, and that they are not suitable for use in all situations. In particular when, the data set is skewed (not normally distributed; more on this later) or has outliers (a value or values that are well above or below the majority of the data) the mean and standard deviation do not accurately describe the data. For example, suppose that the vast majority of residents described in Table 1 are aged between \(40\) and \(45\), but that there is a very small group of residents aged in their \(80\)s. The latter ages would be outliers, and would cause the mean to increase above what would otherwise be the central value. In such instances the median is a more appropriate measure of central tendency (as it is not affected by outliers or skew), and the interquartile range is the accompanying measure of dispersion. So if a variable is skewed or has outliers a good piece of research will make use of the median and interquartile range as the summary measures instead.

If you would like to learn more about descriptive statistics for continuous variables, including how to calculate them, please refer to the Descriptive statistics for one continuous variable section of this module. Otherwise, to practise interpreting descriptive statistics for continuous variables have a go at the following question.

Interpreting inferential statistics

Inferential statistics are used to draw inferences about the wider population when data is obtained from a sample of that population, rather than from the whole population (as the latter is usually not feasible). There are lots of different inferential statistical tests, for different kinds of analysis and for different kinds of variables. For example, different tests are used for continuous and categorical variables and different tests are used for continuous variables depending on their sample size or distribution (pattern or spread of the data).

One example of a distribution that may influence the type of test used is the normal distribution. This is a special kind of distribution that large amounts of naturally occurring continuous data often approximates, and which has two key properties; that the mean, median and mode are all equal, and that fixed proportions of the data lie within certain standard deviations of the mean (\(68\%\) within one SD, \(95\%\) within two SDs and \(99.7\%\) within three SDs). When the sample size is small (typically considered below about 30), or sometimes even when it isn’t, researchers will check to see if continuous variables conform to this distribution. While this isn’t always reported on, when it is the Shapiro-Wilk test (one of a series of tests used for checking normality) is usually referred to. If an article states that variables pass this test (or more specifically, that the \(p\) value for this hypothesis test is above \(.05\)) it means that normality can be assumed. For example, Power et al. (2019) reference this when they state that the “outcomes were assessed for normality using Shapiro-Wilk” (p. 5). Other times an article might state that variables have been transformed (with a natural logarithm for example), which means that while the variables were not originally normally distributed, they have had a mathematical function applied to them which has made them so (if you would like more information on the properties of the normal distribution, and how to assess whether a variable is normally distributed, please refer to The normal distribution page of this module).

If continuous variables are normally distributed or can be transformed so that they are, or if the sample size is large enough for this not to be an issue, parametric tests are used to analyse them. Alternatively, if the sample size is small and variables are not normally distributed, or if the variables are categorical, nonparametric tests are used instead. Some examples of parametric tests include \(t\) tests, ANOVA and Pearson’s correlation, while some examples of nonparametric tests include chi-square tests, the Mann-Whitney U Test, the Wilcoxon Signed Rank Test, the Kruskal-Wallis One-Way ANOVA and Spearman’s Rho.

For each of these tests, a good article should include statistics that show whether any differences or relationships between variables can be considered statistically and/or practically significant in terms of the population. These terms, the relevant statistics, and how to interpret them are explained below. Alternatively, for more information on inferential statistics, including how to calculate measures of statistical and practical significance, please refer to the Inferential statistics page of this module.

Interpreting statistical significance

Statistical significance refers to the likelihood that what has been observed in the sample (for example a difference in means or a relationship between variables) could have occurred due to random chance alone. In particular, if it is very unlikely that it could have been due to chance alone then it is considered statistically significant in the population. What do we mean by ‘very unlikely’ though? This is where the \(p\) value comes in!

The \(p\) value is the probability that what has been observed could be due to random chance alone, so the lower the \(p\) value, the less likely it is that the results are due to chance. Furthermore, the value that is used as the ‘cut-off’ value to decide whether the probability is low enough or not is called the level of significance, and is denoted by \(\alpha\). Different articles may use different levels of significance, but a very common value is \(.05\). In this case, a \(p\) value less than or equal to \(.05\) means that the results are statistically significant. Other common levels of significance used are \(.01\) and \(.001\), and the article may state what level of significance the results are statistically significant at (for example, that they are statistically significant at the \(.05\) or \(.01\) level).

Note that articles will also often include confidence intervals in addition to \(p\) values. These are ranges of values that a population statistic is expected to lie between with a given level of certainty, which is usually \(95\%\) (in which case it is referred to as a \(95\%\) confidence interval). Confidence intervals can also be used to determine statistical significance (at the \(.05\) level of significance for a \(95\%\) confidence interval), and have the added benefit of providing extra information (for example, the magnitude and direction of a difference between means).

As an example of both \(p\) values and confidence intervals consider Table 2, which displays descriptive statistics together with \(p\) values and confidence intervals for a series of variables. The latter two statistics enable us to determine if there is a statistically significant difference in means between the two groups (adolescents with and without cerebral palsy) at the .05 level of significance for each of the variables.

Table 2
Descriptive statistics, \(95\%\) CIs and \(p\) values for a study investigating mental and physical health of adults with cerebral palsy

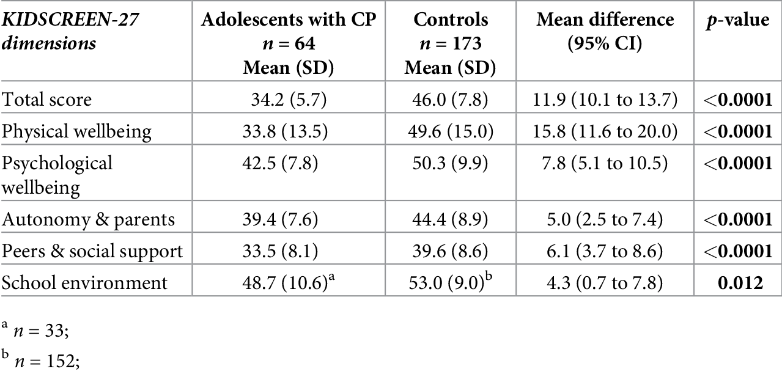
From “Health-Related Quality of Life and Mental Health of Adolescents with Cerebral Palsy in Rural Bangladesh,” by R. Power, M. Muhit, E. Heanoy, T. Karim, N. Badawi, R. Akhter, & G. Khandaker, 2019, PLOS One , 14 (6), p. 9 (https://doi.org/10.1371/journal.pone.0217675). CC-BY.

As an example let’s consider at the ‘Total score’ variable, which is the total score on a questionnaire regarding health-related quality of life. The mean difference of \(11.9\) is the difference in ‘Total score’ means between those with cerebral palsy and those without in the sample, and this is a descriptive statistic. The \(95\%\) confidence interval of \(10.1\) to \(13.7\) indicates that we are \(95\%\) confident the sample has come from a population where the difference in means is somewhere between \(10.1\) and \(13.7\), and the fact that this \(95\%\) confidence interval does not include the value of \(0\) (which would indicate no difference in the means) indicates that the difference in means between the two groups is statistically significant at the \(.05\) level of significance.

The fact that \(p < .0001\) also tells us that the difference in means between the two groups is statistically significant, not only at the \(.05\) level of significance but even at the \(.0001\) level of significance. The statistics for the remaining variables can be analysed in the same way; to practise doing this, have a go at the following questions.

Interpreting practical significance

Practical significance refers to whether something observed in a sample (for example a difference in means or a relationship between variables) is meaningful in a practical sense or not. It is determined by calculating an effect size , which is different for different tests. For example:

• Cohen’s d is a measure of effect size for \(t\) tests
• Pearson’s correlation coefficient is a measure of effect size for Pearson’s correlation
• Phi, Cramer’s V, odds ratio and relative risk are common measures of effect size for the chi-square test of independence.

Articles that report on practical significance provide an important additional perspective to those that only report on statistical significance, as the latter alone does not allow the reader to have an appreciation of whether the findings are important in a real-life sense or not. In particular, the fact that statistical significance is influenced by sample size means that in very large samples, very small differences that are not actually meaningful in real life may be found to be statistically significant, and conversely in very small samples, very large differences that are meaningful in real life may not be found to be statistically significant. This relates to the statistical power of a test, which is the probability that an effect of a certain size will be found to be statistically significant. In particular, a calculation can be performed to determine how big a sample needs to be in order to observe an effect of a certain size at a certain level of significance for a given power (usually \(0.8\) or above), so articles may also refer to the power of a test.

Returning to measures of effect size, and as an example consider Table 3 which shows odds ratios in addition to \(95\%\) confidence intervals and \(p\) values. The latter two relate to the statistical significance of the association between each exposure variable and the outcome variable (L.longbeachae infection), while the odds ratios relate to the practical significance of the association.

Table 3
Odds ratios, \(95\%\) CIs and \(p\) values for a study investigating L.longbeachae infection exposures involving potting mix

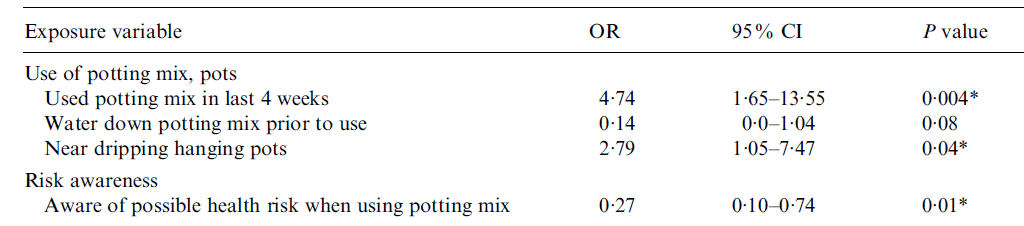
From “Does using Potting Mix make you Sick? Results from a Legionella Longbeachae Case-Control Study in South Australia,” by B. A. O’Connor, J. Carman, K. Eckert, G. Tucker, R. Givney, & S. Cameron, 2007, Epidemiology and Infection , 135 (1), p. 36 (https://doi.org/10.1017/S095026880600656X). Copyright 2006 by Cambridge University Press.

For each exposure variable listed, the odds ratio compares the odds of exposure (relative to non-exposure) in the group with L.longbeachae infection, with the odds of exposure (relative to non-exposure) in the group without L.longbeachae infection. In other words, each odds ratio specifies how many times more or less likely those with L.longbeachae infection were to have the exposure than those without L.Longbeachae infection. An odds ratio less than \(1\) means that the group with the L.longbeachae infection are less likely to have the exposure, an odds ratio of \(1\) means that the two groups are equally likely to have the exposure, and an odds ratio greater than \(1\) means that the group with the L.longbeachae infection are more likely to have the exposure.

For example, the first odds ratio of \(4.74\) indicates that those infected with L.longbeachae were \(4.74\) times more likely to have used potting mix in the last four weeks than those not infected. According to Cohen’s conventions for interpreting effect size detailed here this indicates a medium to large effect, although note that this kind of interpretation is contextual and that interpreting practical significance is less concerned with comparing to cut-off values than statistical significance.

Furthermore, the first \(95\%\) confidence interval of \(1.65 - 13.55\) indicates that we are \(95\%\) confident that this sample comes from a population where those infected with L.longbeachae were somewhere between \(1.65\) and \(13.55\) times more likely to have used potting mix in the last four weeks than those not infected. As this confidence interval does not include the value of \(1\) (which for an odds ratio means that the odds of exposure are the same for those with and without the outcome), the association between using potting mix in the last four weeks and L.longbeachae infection is statistically significant at the \(.05\) level of significance. This is also evidenced by the \(p\) value of \(.004\).

Note that articles will often include adjusted odds ratios in addition to, or in place of, the (crude) odds ratios seen above. These are odds ratios that have been adjusted to take into account any additional confounding variables (i.e. other variables that may be having an influence on the outcome variable), and can be interpreted in the same way.

If you would like to practise interpreting some of the other odds ratios in the table, have a go at the following questions.

Further example: interpreting one-way ANOVA

As another example of interpreting statistical and practical significance, consider Tables 4 and 5. These show the results of two one-way ANOVAs, used to test for significant differences in mean ‘school attachment scores’ between students of different ages and between students of different socio-economic statuses respectively.

Table 4
Descriptive statistics and one-way ANOVA statistics for a study investigating differences in school attachment scores between age groups

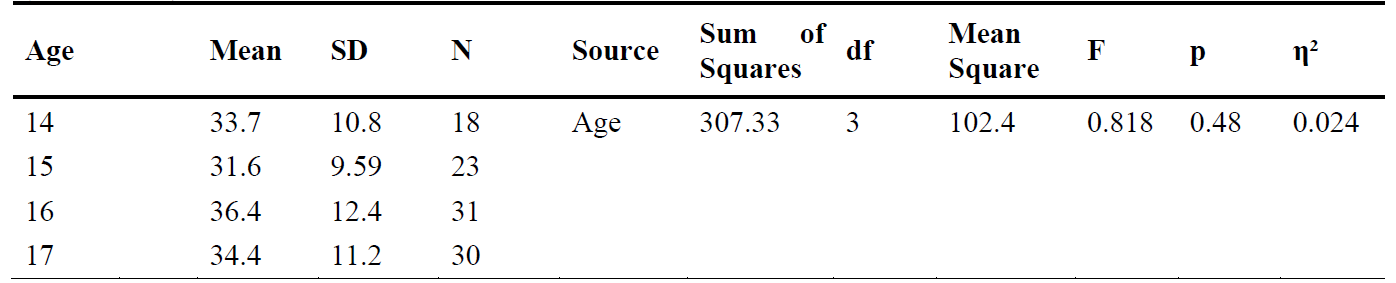
Table 5
Descriptive statistics and one-way ANOVA statistics for a study investigating differences in school attachment scores between socio-economic groups

From “School Attachment and Video Game Addiction of Adolescents with Divorced vs. Married Parents,” by B. TAS, 2019, TOJET: The Turkish Online Journal of Educational Technology , 18 (2), pp. 99-100 (https://files.eric.ed.gov/fulltext/EJ1211160.pdf). Copyright 2019 by The Turkish Online Journal of Educational Technology.

The \(p\) value for each one-way ANOVA indicates either that there is a statistically significant difference between the means of at least two of the groups (if \(p\) is less than or equal to the level of significance), or that there is no statistically significant difference in the means between any of the groups (if \(p\) is greater than the level of significance). Note that if a one-way ANOVA is statistically significant further information is needed, and should be provided, to determine which groups are significantly different from each other. This will either be the results of a planned or post hoc comparison, both of which will provide further \(p\) values which can be interpreted in the usual way.

These tables also include (amongst other statistics) an \(F\) value for each one-way ANOVA. This is the test statistic for this test (note that results of other tests will sometimes include the test value as well; a \(t\) value for a \(t\) test or chi-square value for a chi-square test of independence, for example). This \(F\) value is the ratio of the variability between groups to the variability within each group. For example, an \(F\) value of \(0.818\) for the ‘Age’ variable indicates that the variability in school attachment scores between the four age groups is \(0.818\) times the variability in school attachment scores within each age group (i.e. the variability between the groups is actually less than the variability within the groups). The bigger than \(1\) the \(F\) value is, the greater the likelihood that there is a significant difference in the means between at least two of the groups. However, note that it is the \(p\) value that needs to be interpreted in order to test this.

Lastly, the tables also include eta-squared (\(\eta^2\)) values as measures of effect size, which indicate how much variability (as a percentage) in the school attachment scores can be attributed to age and socio-economic status respectively. For example, the \(\eta^2\) value of \(0.024\) indicates that \(2.4\%\) of the variability in the school attachment scores can be attributed to age. Cohen (1988) suggests that an \(\eta^2\) value of \(.01\) be considered a small effect, \(.059\) be considered a medium effect and \(.138\) be considered a large effect.

Use the information above to answer the following questions:

References

Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Lawrence Erlbaum Associates, Inc.

Connor, B.A., Carman, J., Eckert, K., Tucker, G., Givney, R., & Cameron, S. (2007). Does using potting mix make you sick? Results from a Legionella longbeachae case-control study in South Australia. Epidemiology and Infection, 135 (1), 34-39. https://doi.org/10.1017/S095026880600656X

Power, R., Muhit, M., Heanoy, E., Karim, T., Badawi, N., Akhter, R., & Khandaker, G. (2019). Health-related quality of life and mental health of adolescents with cerebral palsy in rural Bangladesh. PLoS One, 14 (6), 1-17. https://doi.org/10.1371/journal.pone.0217675

TAS, B. (2019). School attachment and video game addiction of adolescents with divorced vs. married parents. TOJET : The Turkish Online Journal of Educational Technology , 18 (2), 93-106. https://files.eric.ed.gov/fulltext/EJ1211160.pdf

Visram, S., Smith, S., Connor, N., Greig, G., & Scorer, C. (2018). Examining associations between health, wellbeing and social capital: Findings from a survey developed and conducted using participatory action research. Journal of Public Mental Health, 17 (3), 122-134. https://doi.org/10.1108/JPMH-09-2017-0035