Introduction to statistics

One reason for conducting a hypothesis test is to determine whether there is a statistically significant difference between means. You might compare the mean of a single sample with a constant value, or compare the means of two or more independent or related samples. Different statistical tests are used depending on the type of comparison being made. This page explains some of the most common tests, along with non-parametric alternatives that compare mean ranks for ordinal data.

One sample \(t\) test

A one sample \(t\) test is used to test whether the mean of a continuous variable in a population is significantly different from a particular value. This value, which is often obtained from previous research, is called the test value. For example, suppose you have a sample of student final marks and want to test whether the students come from a population with a mean final mark equal to the previous year’s mean of \(70\). In this case, the hypotheses for a two-tailed hypothesis test would be:

\(\textrm{H}_\textrm{0}\): The sample comes from a population with a mean final mark of \(70\) (\(\mu_{\textrm{final mark}} = 70\))
\(\textrm{H}_\textrm{A}\): The sample does not come from a population with a mean final mark of \(70\) (\(\mu_{\textrm{final mark}} \neq 70\))

Before conducting a one sample \(t\) test, you need to check that the following assumptions are met:

If the assumptions for the one sample \(t\) test are not met, the one sample Wilcoxon signed-rank test may be an appropriate non-parametric alternative. This test uses the ranks of the data.

If the assumptions for the one sample \(t\) test are met, you can conduct the test using statistical software, such as SPSS. The results should include the following statistics:

When analysing the results, first look at the descriptive statistics to get an idea of what is happening in the sample. In this example, the sample mean is \(73.40\) as shown in the first table. The test value is \(70\), giving a difference of \(3.40\). This is shown as the mean difference in the second table.

To determine whether this difference is statistically significant, we need to look at the \(p\) value and the confidence interval for the difference. The \(p\) value is shown as ‘Sig. (2-tailed)’ in the second table because we have conducted a two-tailed hypothesis test. If we are using a level of significance of \(.05\):

• If \(p \leqslant .05\), we reject \(\textrm{H}_\textrm{0}\) and conclude that the population mean is significantly different from the test value.
• If \(p > .05\) we do not reject \(\textrm{H}_\textrm{0}\) and conclude that the population mean is not significantly different from the test value.

In this case, our \(p\) value of \(.025\) indicates that the difference is statistically significant.

This is also shown by the confidence interval of (\(.45\), \(6.36\)) for the difference between the population mean and our test value of \(70\). Because this confidence interval does not contain zero, the difference is statistically significant. In fact, we are \(95\%\) confident that the true population mean is between \(.45\) and \(6.36\) points higher than our test value.

Note that the test statistic (\(t\)) and degrees of freedom (\(df\)) should generally be reported as part of your results. However, you do not need to interpret these when deciding whether the difference is statistically significant.

If you would like to practise interpreting the results of a one sample \(t\) test for statistical significance, have a go at one or both of the following activities.

To evaluate practical significance when using a one sample \(t\) test, Cohen’s \(d\) is often used to measure the effect size. This tells us how many standard deviations the sample mean is from the test value. Cohen’s \(d\) can also usually be obtained using statistical software. For example, the Cohen’s \(d\) for our final mark data is included in the following output:

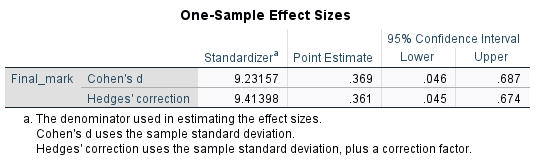
This tells us that our sample mean is \(0.37\) standard deviations from the test value, indicating a small to medium effect. As a general guide, a Cohen’s \(d\) with a magnitude of \(0.2\) is considered small, \(0.5\) medium and \(0.8\) or above large.

Paired samples \(t\) test

A paired samples \(t\) test is used to test whether there is a significant difference between the means of a continuous variable measured for two related groups or under two related conditions. For example, suppose you have a sample of individuals whose heart rate is recorded twice, before and after exercise. You could use a paired samples \(t\) test to determine whether there is a significant difference between the mean heart rate before and after exercise. In this case, the hypotheses for a two-tailed hypothesis test would be:

\(\textrm{H}_\textrm{0}\): There is no significant difference in mean heart rate before and after exercise
(\(\mu_{\textrm{HR before}} = \mu_{\textrm{HR after}}\), or \(\mu_{\textrm{HR before}} - \mu_{\textrm{HR after}} = 0\))

\(\textrm{H}_\textrm{A}\): There is a significant difference in mean heart rate before and after exercise
(\(\mu_{\textrm{HR before}} \neq \mu_{\textrm{HR after}}\), or \(\mu_{\textrm{HR before}} - \mu_{\textrm{HR after}} \neq 0\))

Before conducting a paired samples \(t\) test, you need to check that the following assumptions are met:

If the assumptions for the paired samples \(t\) test are not met, the Wilcoxon signed-rank test may be an appropriate non-parametric alternative. This test uses the ranks of the data.

If the assumptions for the paired samples \(t\) test are met, you can conduct the test using statistical software, such as SPSS. The results should include the following statistics:

When analysing the results, first look at the descriptive statistics to get an idea of what is happening in the sample. In this example, the difference between the before and after sample means is \(-48.70\). This value can be calculated from the means in the first table and is also shown in the second table. The negative value simply indicates that the mean heart rate after exercise is higher than the mean heart rate before exercise.

To determine whether this difference is statistically significant, we need to look at the \(p\) value and the confidence interval for the difference. The \(p\) value is shown as ‘Sig. (2-tailed)’ in the second table because we have conducted a two-tailed hypothesis test. If we are using a level of significance of \(.05\):

• If \(p \leqslant .05\) we reject \(\textrm{H}_\textrm{0}\) and conclude that the population means for the two related groups are significantly different.
• If \(p > .05\) we do not reject \(\textrm{H}_\textrm{0}\) and conclude that the population means for the two related groups are not significantly different.

In this case, our \(p\) value of \(< .001\) indicates that the difference between the means is statistically significant.

his is also shown by the confidence interval of (\(-52.65\), \(-44.75\)) for the difference between the means. Because this confidence interval does not contain zero, the difference is statistically significant. In fact, we are \(95\%\) confident that the population mean heart rate after exercise is between \(44.75\) and \(52.65\) bpm higher than the population mean heart rate before exercise.

Note that the test statistic (\(t\)) and degrees of freedom (\(df\)) should generally be reported as part of your results. However, you do not need to interpret these when deciding whether the difference is statistically significant.

If you would like to practise interpreting the results of a paired samples \(t\) test for statistical significance, have a go at one or both of the following activities.

To evaluate practical significance when using a paired samples \(t\) test, Cohen’s \(d\) can again be used to measure the effect size. In this case, it measures the size of the mean difference in standard deviation units and can usually be obtained using statistical software. For example, the Cohen’s \(d\) for our heart rate data is included in the following output:

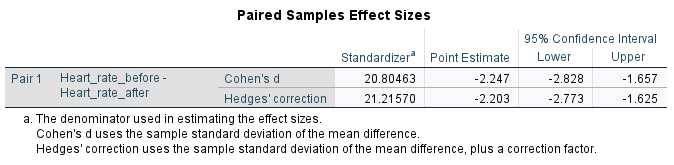
This tells us that the difference between the two sample means is \(3.95\) standard deviations, indicating a very large effect. As a general guide, a Cohen’s \(d\) with a magnitude of \(0.2\) is considered small, \(0.5\) medium and \(0.8\) or above large.

Independent samples \(t\) test

An independent samples \(t\) test is used to test whether there is a significant difference between the means of a continuous variable for two independent groups. For example, suppose you collect data on the number of hours males and females spend watching TV each week. You could use an independent samples \(t\) test to determine whether there is a significant difference between the mean hours for the two groups. In this case, the hypotheses for a two-tailed hypothesis test would be:

\(\textrm{H}_\textrm{0}\): There is no significant difference in mean TV hours per week for males and females
(\(\mu_{\textrm{males}} = \mu_{\textrm{females}}\), or \(\mu_{\textrm{males}} - \mu_{\textrm{females}} = 0\))

\(\textrm{H}_\textrm{A}\): There is a significant difference in mean TV hours per week for males and females
(\(\mu_{\textrm{males}} \neq \mu_{\textrm{females}}\), or \(\mu_{\textrm{males}} - \mu_{\textrm{females}} \neq 0\))

Before conducting an independent samples \(t\) test, you need to check that the following assumptions are met:

If the assumptions of the independent samples \(t\) test are not met, the Mann-Whitney U test may be an appropriate non-parametric alternative. This test uses the ranks of the data.

If the assumptions for the independent samples \(t\) test are met, you can conduct the test using statistical software, such as SPSS. The results should include the following statistics:

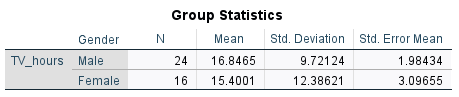
When analysing the results, first look at the descriptive statistics to get an idea of what is happening in the sample. In this example, the difference between the sample means for males and females is \(1.45\). This value can be calculated from the means in the first table and is also shown in the second table.

Next, you need to determine which row of the second table to use. The top row is used when the variances of the two groups can be assumed to be equal. The bottom row is used when the variances cannot be assumed to be equal. Each row provides a one-sided and two-sided \(p\) value. Because we are conducting a two-tailed hypothesis test, we will use the two-sided \(p\) value.

To determine which row to use, first look at the \(p\) value for Levene’s Test for Equality of Variances, shown in the ‘Sig.’ column. The null hypothesis for this test is that the variances are equal. Therefore:

• If \(p \leqslant .05\) we reject \(\textrm{H}_\textrm{0}\) and use the Equal variances not assumed row.
• If \(p > .05\) we do not reject \(\textrm{H}_\textrm{0}\) and use the Equal variances assumed row.

In this example, the \(p\) value for Levene’s test is \(.257\). This means that we do not reject the null hypothesis that the variances are equal. We therefore use the two-sided \(p\) value and confidence interval in the Equal variances assumed row. The interpretation of this \(p\) value is:

• If \(p \leqslant .05\) we reject \(\textrm{H}_\textrm{0}\) and conclude that the population means of the two groups are significantly different.
• If \(p > .05\) we do not reject \(\textrm{H}_\textrm{0}\) and conclude that the population means of the two groups are not significantly different.

In this case, our \(p\) value of \(.682\) indicates that the difference between the means is not statistically significant.

This is also shown by the confidence interval of \(-5.64, 8.54\) for the difference between the means. Because this confidence interval contains zero, the difference is not statistically significant. In fact, we are \(95\%\) confident that the difference in mean hours spent watching TV each week for males and females is between \(-5.64 and 8.54\) hours.

Note that the test statistic (\(t\)) and degrees of freedom (\(df\)) should generally be reported as part of your results. However, you do not need to interpret these when deciding whether the difference is statistically significant.

If you would like to practise interpreting the results of an independent samples \(t\) test for statistical significance, have a go at one or both of the following activities.

To evaluate practical significance when using an independent samples \(t\) test, Cohen’s \(d\) can again be used to measure the effect size. In this case, it measures the difference between the two means in standard deviation units and can usually be obtained using statistical software. For example, the Cohen’s \(d\) for our TV hours data is included in the following output:

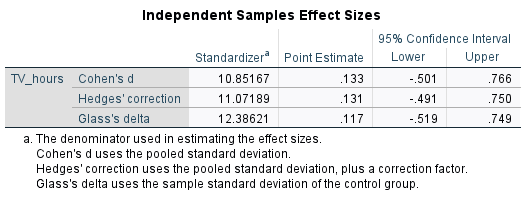
This tells us that our two sample means are separated by \(0.13\) standard deviations, indicating a very small effect. As a general guide, a Cohen’s \(d\) with a magnitude of \(0.2\) is considered small, \(0.5\) medium and \(0.8\) or above large.

One-way ANOVA

One-way ANOVA is similar to the independent samples \(t\) test but is used to compare the means of three or more independent groups. One-way ANOVA is the only type of ANOVA covered here. However, it is part of a family of ANOVA tests that also includes:

• Factorial ANOVA: used to test for differences in means between groups when there are two or more independent variables.
• One-way repeated measures ANOVA: used to test for differences in means between three or more related samples.
• ANCOVA (one-way analysis of covariance): used to test for differences between two or more independent samples after controlling for the effects of a third variable (covariate).
• MANOVA (multivariate analysis of variance): used to test for differences between groups on multiple dependent variables at the same time.

Returning to the one-way ANOVA, suppose you have a data set containing the final marks of a sample of students studying one of three different units. You could use a one-way ANOVA to determine whether there is a significant difference between the mean marks for any of the units. In this case, the hypotheses would be:

\(\textrm{H}_\textrm{0}\): There is no significant difference in the mean final mark for any of the three units.
(\(\mu_{\textrm{unit 1}} = \mu_{\textrm{unit 2}} = \mu_{\textrm{unit 3}}\))

\(\textrm{H}_\textrm{A}\): The mean final mark of at least one of the units is significantly different to the others.

Before conducting a one-way ANOVA, you need to check that the following assumptions are met:

If the assumptions of the one-way ANOVA are not met, another test may be more appropriate. If the normality assumption is not met, the Kruskal-Wallis test may be an appropriate non-parametric alternative. This test uses the ranks of the data. If the equal variances assumption is not met, the Brown-Forsythe or Welch test can be used instead.

If the assumptions for the one-way ANOVA are met, you can conduct the test using statistical software, such as SPSS. The results should include the following statistics:

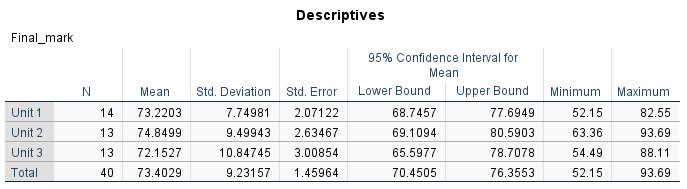
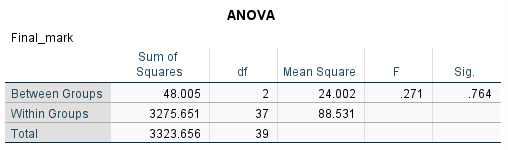
When analysing the results, first look at the descriptive statistics to get an idea of what is happening in the sample. In this example, the sample means are \(73.22\) for Unit 1, \(74.85\) for Unit 2 and \(72.15\) for Unit 3. To determine whether there is a statistically significant difference between these means, we need to look at the \(p\) value, which is shown as ‘Sig.’ in the second table. If we are using a level of significance of \(.05\):

• If \(p \leqslant .05\) we reject \(\textrm{H}_\textrm{0}\) and conclude that the mean of at least one of the groups is significantly different from the others.
• If \(p > .05\) we do not reject \(\textrm{H}_\textrm{0}\) and conclude that there are no statistically significant differences between the group means.

In this case, our \(p\) value of \(.764\) indicates that there are no statistically significant differences in mean final marks between the units.

Note that the test statistic (\(F\)) and degrees of freedom (\(df\)) should generally be reported as part of your results. However, you do not need to interpret these when deciding whether the difference is statistically significant.

If a one-way ANOVA shows that at least one of the means is significantly different, you will need to investigate further to determine which groups are different. This can be done using post hoc tests, such as Tukey’s HSD.

For now though, if you would like to practise interpreting the results of a one-way ANOVA for statistical significance, have a go at one or both of the following activities.

To evaluate practical significance when using a one-way ANOVA, eta-squared can be used to measure the effect size. This indicates how much of the variability in the dependent variable can be attributed to the independent variable, expressed as a percentage. It can also usually be obtained using statistical software. For example, the eta-squared for our final mark data is included in the following output:

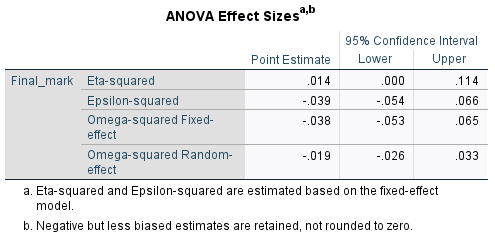
The eta-squared value of \(0.014\) tells us that \(1.4\%\) of the variability in final marks can be attributed to the unit of study. This indicates a small effect. As a general guide, an eta-squared of \(0.01\) is considered small, \(0.059\) medium, and \(0.138\) or above large.