Geometry and trigonometry
Geometry is the branch of mathematics that explores the properties of shapes, angles and lines.
This page provides an introduction to different types of angles, different kinds of shapes and lines of symmetry, while subsequent pages provide information on further properties of triangles, as well as on calculating perimeter and area of two-dimensional shapes and surface area, volume and density of three-dimensional shapes.
Angles
An angle is the amount of rotation between two lines that intersect at a point. For example, there is an angle between the lines \(AB\) and \(AC\) in the diagram below, and we can refer to this as either \(\angle CAB\) or \(\angle A\)
Angles are commonly measured in degrees, denoted by \(^\circ\), whereby one full rotation is equal to \(360^\circ.\) Note that angles can also be measured in radians, where \(\pi\,\textrm{rad} = 180^\circ\) and \(2\pi\,\textrm{rad} = 360^\circ,\) however only degrees will be used in this module.
There are names for different angles depending on their size, with some of the most common ones to be aware of as follows:
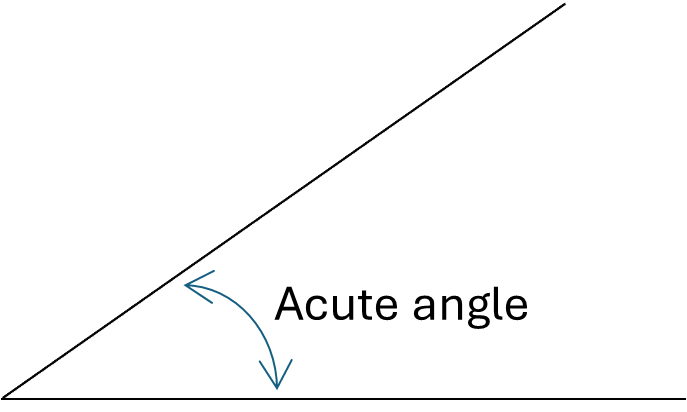
Acute angles are angles that are less than \(90^\circ\)
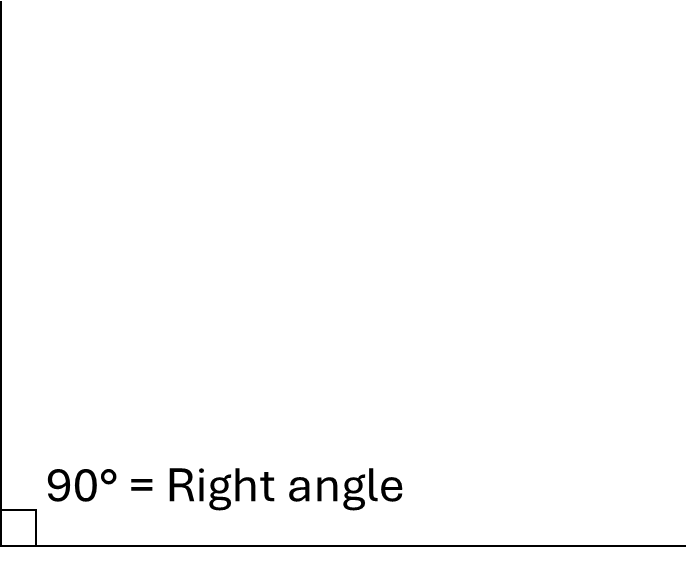
Right angles are angles that are equal to \(90^\circ\) (note the little square used to represent this)
Obtuse angles are angles that are greater than \(90^\circ\) but less than \(180^\circ\)
\(\)
Furthermore, angles can also be classified according to their sum. Two of the most common examples of this are as follows:
Complementary angles are two angles that sum to \(90^\circ\)
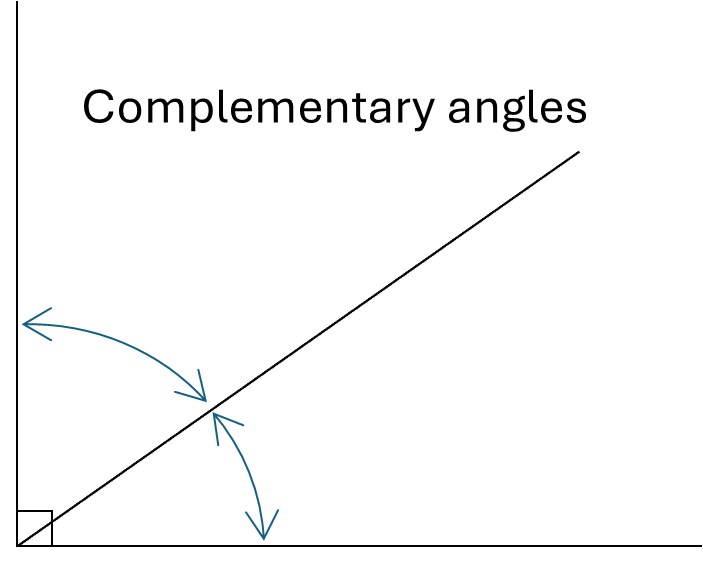
If one angle is known, its complementary angle can be found by subtracting it from \(90^\circ\)
Supplementary angles are two angles that sum to \(180^\circ\)
If one angle is known, its supplementary angle can be found by subtracting it from \(180^\circ\)
\(\)
Check your understanding of different types of angles by completing one or both of the following activities:
The supplementary angle of \(115^\circ\) is \(65^\circ\) since \(180^\circ - 115^\circ = 65^\circ\)
The complementary angle of \(42^\circ\) is \(48^\circ\) since \(90^\circ - 42^\circ = 48^\circ\)
Polygons
Two-dimensional shapes that are bounded by straight lines are called polygons. Furthermore, note that when all the sides of a polygon are the same length and all angles are equal it is called a regular polygon. Details of some common types of polygons are listed in the table below:
| Polygon name | Number of sides | Number of angles | Sum of angles |
|---|---|---|---|
| Triangle | \(3\) | \(3\) | \(180^\circ\) |
| Quadrilateral | \(4\) | \(4\) | \(360^\circ\) |
| Pentagon | \(5\) | \(5\) | \(540^\circ\) |
| Hexagon | \(6\) | \(6\) | \(720^\circ\) |
| Heptagon | \(7\) | \(7\) | \(900^\circ\) |
| Octagon | \(8\) | \(8\) | \(1080^\circ\) |
| Nonagon | \(9\) | \(9\) | \(1260^\circ\) |
| Decagon | \(10\) | \(10\) | \(1440^\circ\) |
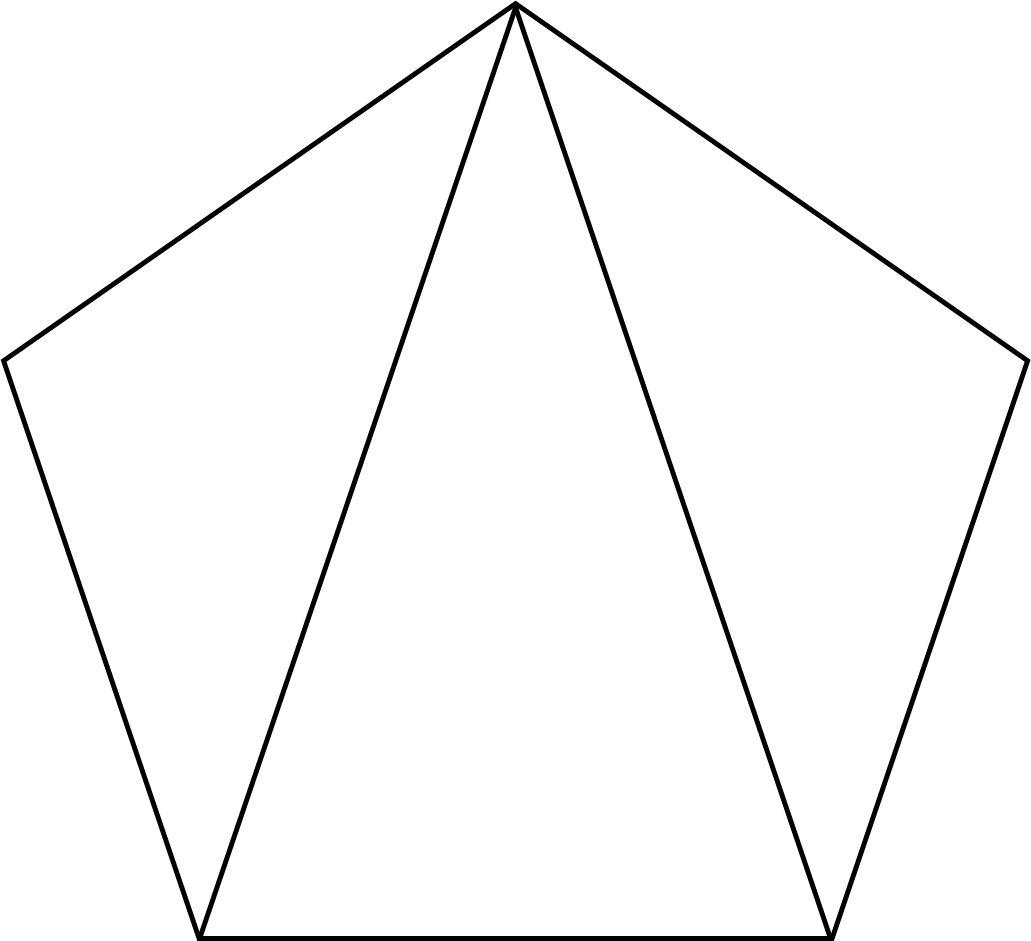
In order to calculate the sum of the internal angles of a polygon, as listed in the table, you can split the polygon into triangles and then multiply the number of triangles formed by \(180^\circ\) (since this is the sum of the angles in a triangle). For example, a pentagon splits into three triangles, as shown below, and \(3 \times 180^\circ = 540^\circ\)
\(\)
Alternatively, you can use the formula \((2n - 4) \times 90^\circ\) to calculate the sum of the angles, where \(n\) is the number of sides of the polygon. For example, the formula can be evaluated to give the same sum of angles for a pentagon as follows:
Check your knowledge of different types of polygons by completing one or both of the following activities:
\(1080^\circ \div 180^\circ = 6\) triangles (or you could draw a diagram to calculate)
\((2 \times 12 - 4) \times 90^\circ = 20 \times 90^\circ = 1800^\circ\) (or you could draw a diagram to calculate)
For details of how to calculate the perimeter and area of some of the polygons listed, see the Perimeter and area page of this module. In addition, see the Trigonometry page if you would like further information about the properties of triangles.
Circles
A circle is a shape created by a continuous curved line which is always the same distance away from a central point. This distance (from the centre of the circle to the outside) is called the radius, while the diameter is the distance from one side of the circle to the other when passing through the centre (i.e. it is double the radius). Finally, the circumference is the distance around the outside of the circle.
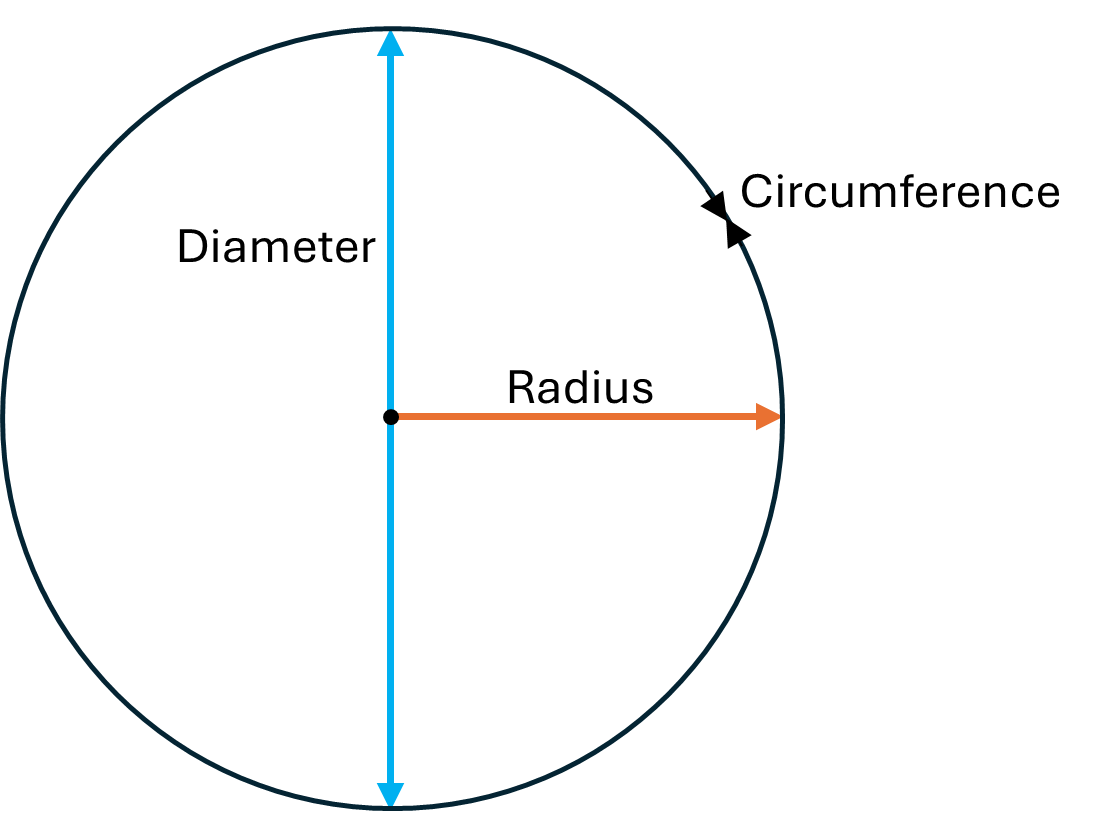
Regardless of the size of the circle, the ratio of the circumference to the diameter is always the same. It is equal to an irrational number called pi (written as \(\pi\)) which is approximately \(3.14\) (note that irrational means that the decimal places in pi go on forever without recurring):
\[\pi = \frac{circumference}{diameter}\]Given this, the circumference of a circle can be calculated if the diameter or radius is known, and vice versa, using the following formulas (where \(c\) represents the circumference, \(d\) the diameter and \(r\) the radius):
\(c = \pi d\)
\(c = 2 \pi r\)
Note that the ‘slice’ of a circle bounded by two radii and an arc of the circumference is called a sector. If the central angle of the sector (i.e. the angle formed by the two radii) is less than \(180^\circ\) it is termed a minor sector, if it is equal to \(180^\circ\) it is a semicircle, and if it is more than \(180^\circ\) it is a major sector.
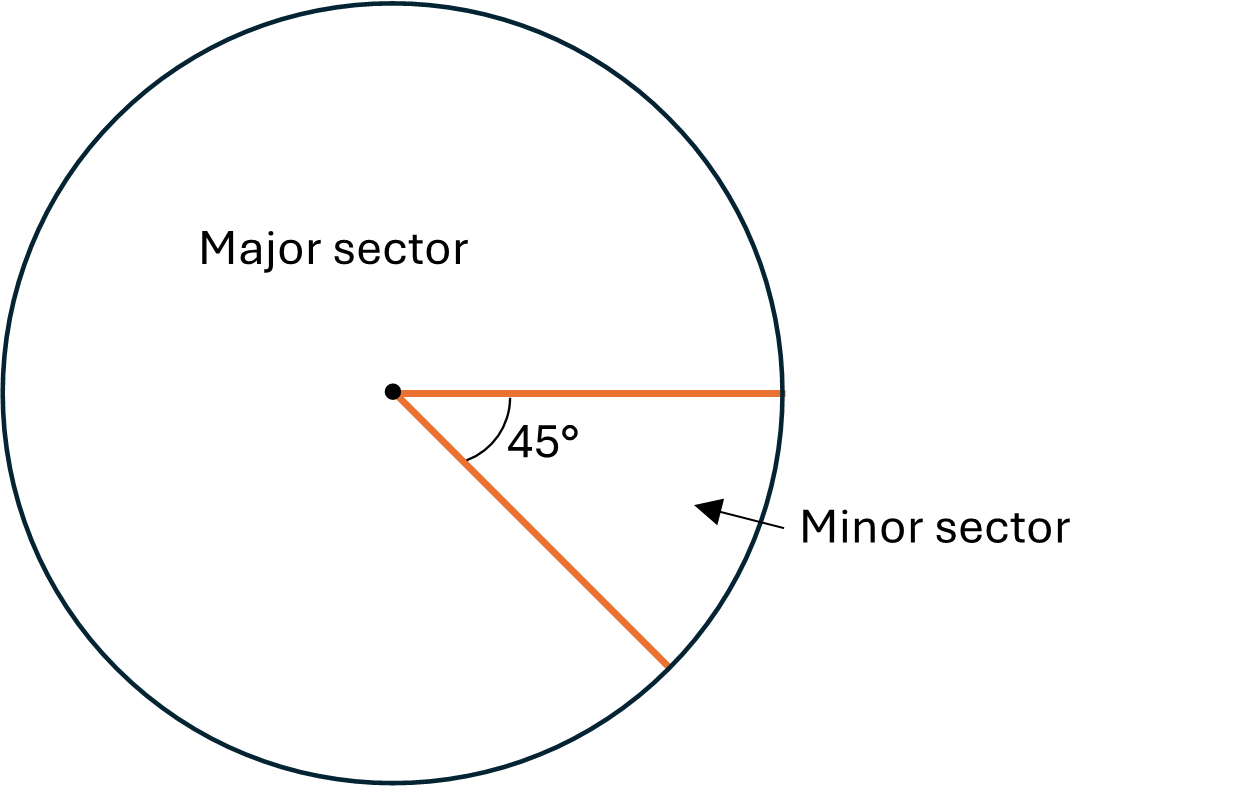
\(\) Check your understanding of the properties of circles by completing one or both of the following activities:
For details of how to calculate the area of a circle or the perimeter or area of a sector of a circle, see the Perimeter and area page of this module.
Three-dimensional shapes
Some common examples of three-dimensional shapes include cubes, prisms, pyramids, cylinders, spheres and cones. These shapes are detailed below, while information about how to calculate the surface area and volume of each is provided in the Surface area, volume and density page of this module.
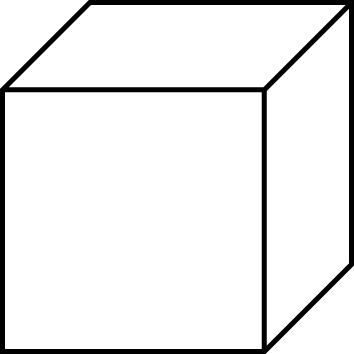
Cubes
A cube is a three-dimensional shape with six identical square faces, each one perpendicular to its adjacent faces. It is a special type of prism.
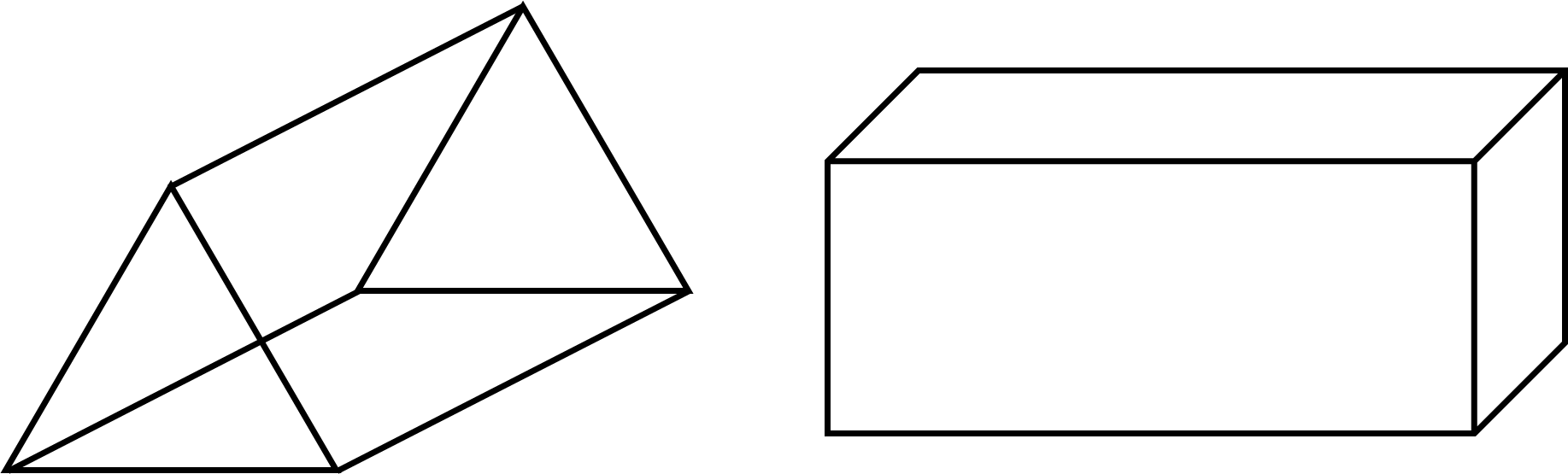
Prisms
A prism is a three-dimensional shape with identical polygon bases (top and bottom faces) and square, rectangle or parallelogram lateral faces (sides). If the bases of a prism are regular polygons the prism is a regular prism, and in this case it is generally named after the polygon. For example, a prism with triangular bases is called a triangular prism, while a prism with rectangular bases is a rectangular prism (also known as a cuboid). Furthermore, note that if either of the bases are missing it is referred to as an open rather than a closed prism.
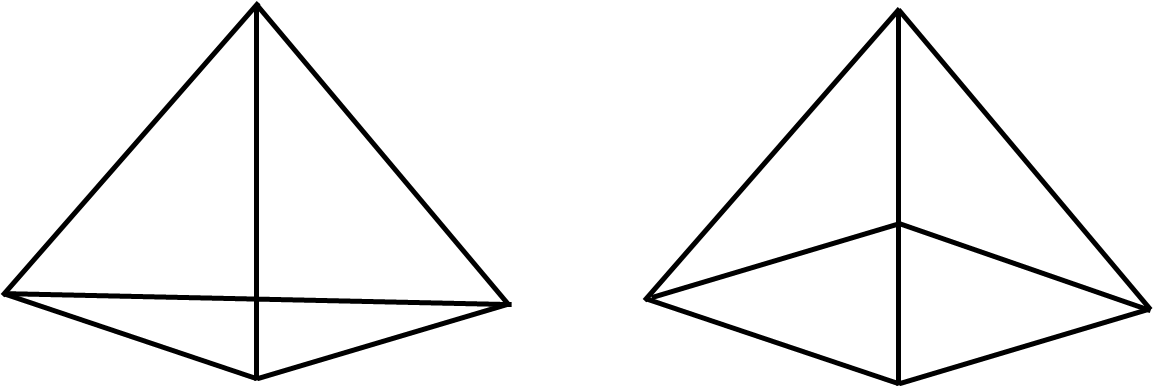
Pyramids
A pyramid is a three-dimensional shape with a polygon base and triangular sides, which meet at a point at the top called the apex. If the base of a pyramid is a regular polygon the pyramid is a regular pyramid, and in this case it is generally named after the polygon. For example, a pyramid with a triangular base is called a triangular pyramid (also known as a tetrahedron, or a regular tetrahedron if all faces are equilateral triangles), while a pyramid with a square base is a square pyramid.
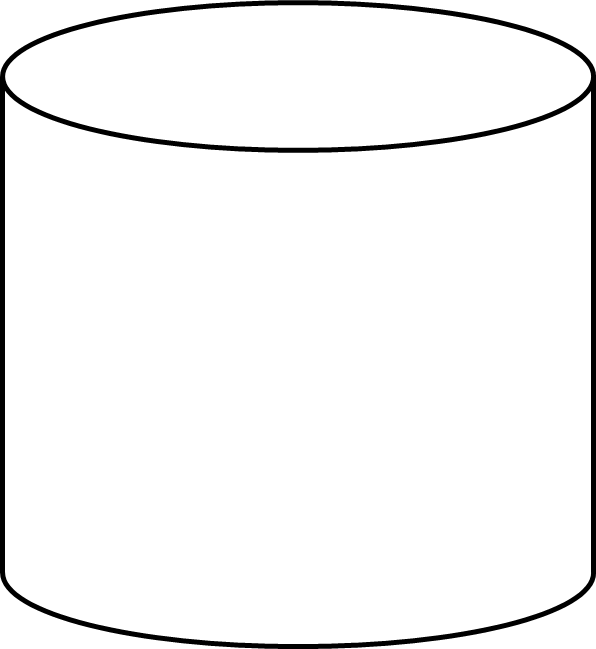
Cylinders
A cylinder is a three-dimensional shape consisting of two identical flat circular ends connected by a curved side. Note that if either of these circular ends are missing, it is referred to as an open rather than a closed cylinder.
Spheres
A sphere is a three-dimensional shape with a curved surface which is always the same distance away from a central point. This distance (from the centre of the sphere to the outside) is called the radius, while the diameter is the distance from one side of the sphere to the other when passing through the centre (i.e. it is double the radius).
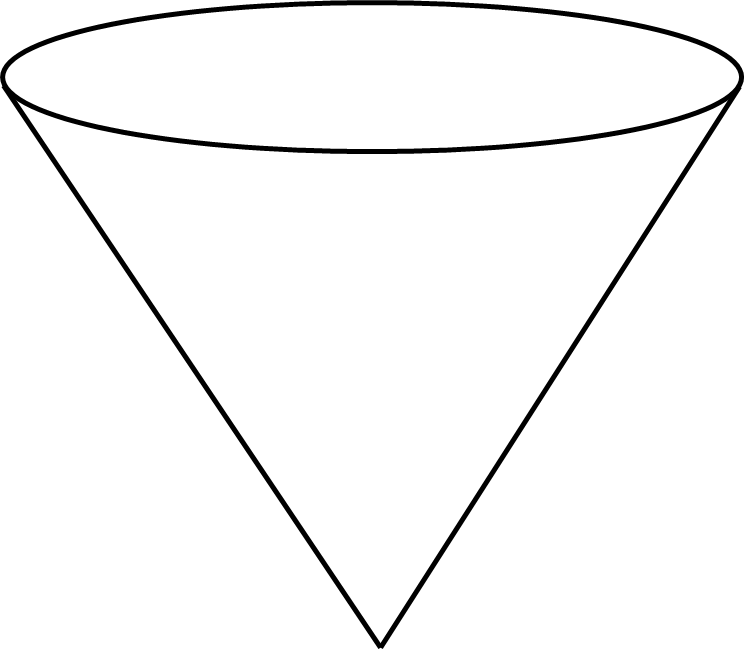
Cones
A cone is a three-dimensional shape with a circular base and a continuous curved surface that tapers to a point called the apex.
Lines of symmetry
If there is at least one line that divides a two-dimensional shape into two identical halves, then that shape is said to have reflection symmetry or line symmetry. The line that divides the figure into two mirror image halves is called the line of symmetry, and this can be in any direction (note that a three-dimensional shape needs to be divided in half by a plane of symmetry rather than a line of symmetry, but this is not covered here). Furthermore, shapes can have more than one line of symmetry, and in particular the number of lines of symmetry in a regular polygon is equal to the number of sides.
Consider the examples of shapes with reflection symmetry below. The dashed lines are the lines of symmetry; note that the triangle has three, while the pentagon has five:
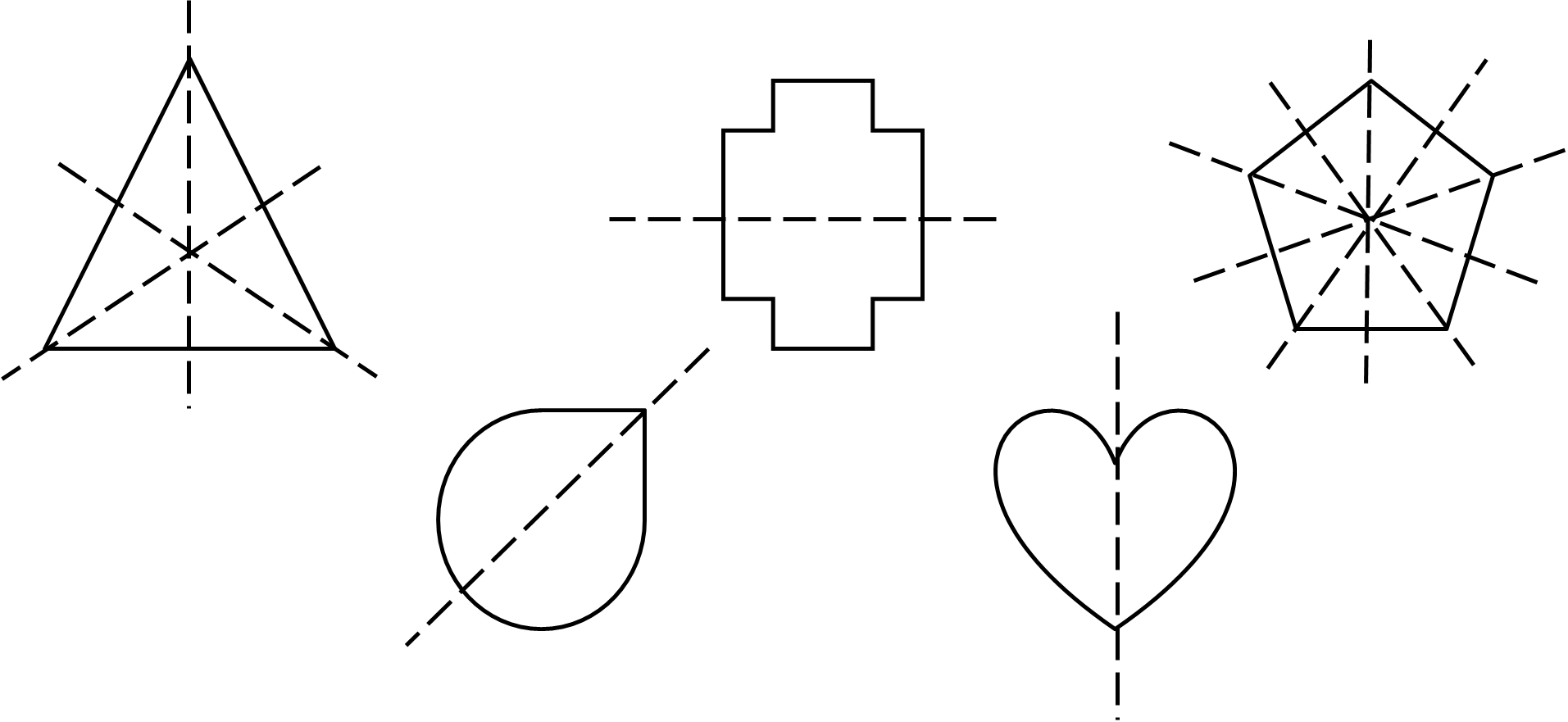
\(\) Check your understanding of lines of symmetry by completing one or both of the following activities:
Seven, as the number of lines of symmetry is equal to the number of sides.
A circle has infinitely many lines of symmetry, as any straight line passing through the centre is a line of symmetry.