Geometry and trigonometry

In brief, this page covers:

• The definition of perimeter, and how to calculate the perimeter of polygons
• The definition of circumference, and how to calculate the circumference of a circle, as well as the perimeter of a sector
• The definition of area, and how to calculate the area of common polygons, circles, and sectors

Example:

Calculate the perimeter of the shape below.

Solution:

To calculate the perimeter we need to add up the value of each side. To do this for the shape above, we first need to determine the values of the three sides that are not labelled.

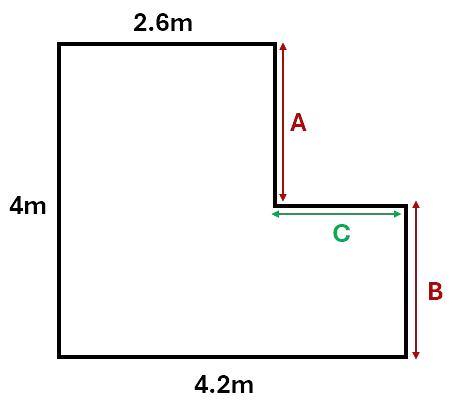
From the image above, we can see that sides A and B together will give us another \(4m\). We can find side C by subtracting \(2.6\) from \(4.2\), therefore C is \(1.6m\).

So the perimeter of the shape will be:

\[P = 2.6 + 4 + 4.2 + 4 + 1.6 = 16.4m\]

The two perimeters of a shape will be:

\[\begin{aligned} External\;perimeter &= internal\;perimeter\;+ \\\ & 2 \times the\;wall\;thickness \times the\;number\;of\;corners \\\ \end{aligned}\] \[\begin{aligned} Internal\;perimeter &= external\;perimeter\;- \\\ & 2 \times the\;wall\;thickness \times the\;number\;of\;corners \\\ \end{aligned}\]

If you know the values of both the external and internal perimeters:

\(Mean\;girth = (external\;perimeter + internal\;perimeter) \div 2\)

If you know the thickness of the wall and the external perimeter:

\[\begin{aligned} Mean\;girth &= external\;perimeter\;-\\\ & the\;wall\;thickness \times the\;number\;of\;corners \\\ \end{aligned}\]

If you know the thickness of the wall and the internal perimeter:

\[\begin{aligned} Mean\;girth &= internal\;perimeter\;+\\\ & the\;wall\;thickness \times the\;number\;of\;corners \\\ \end{aligned}\]

Example 1:

A rectangular brick wall has thickness \(120\,mm\) and internal perimeter \(48\,m\). Calculate the external perimeter.

Solution:

\[\begin{aligned} 120\,mm &= 0.12\,m \\\ External\;perimeter &= internal\;perimeter\;+ \\\ & 2 \times the\;wall\;thickness \times the\;number\;of\;corners \\\ &= 48 + 2 \times 0.12 \times 4 \\\ &= 48.96\,m \\\ \end{aligned}\]

Example 2:

A square room has an external perimeter of \(33.4\,m\) and a thickness of \(0.18\,m\). Calculate the mean girth of the perimeters of this room.

Solution:

\[\begin{aligned} Mean\;girth &= external\;perimeter\;- \\\ & the\;wall\;thickness \times the\;number\;of\;corners \\\ &= 33.4 - 0.18 \times 4 \\\ &= 32.68\,m \\\ \end{aligned}\]

We can calculate the circumference of a circle using the formula:

\[C = 2 \pi r\]

Where \(r\) is the radius, or half the diameter, of the circle.

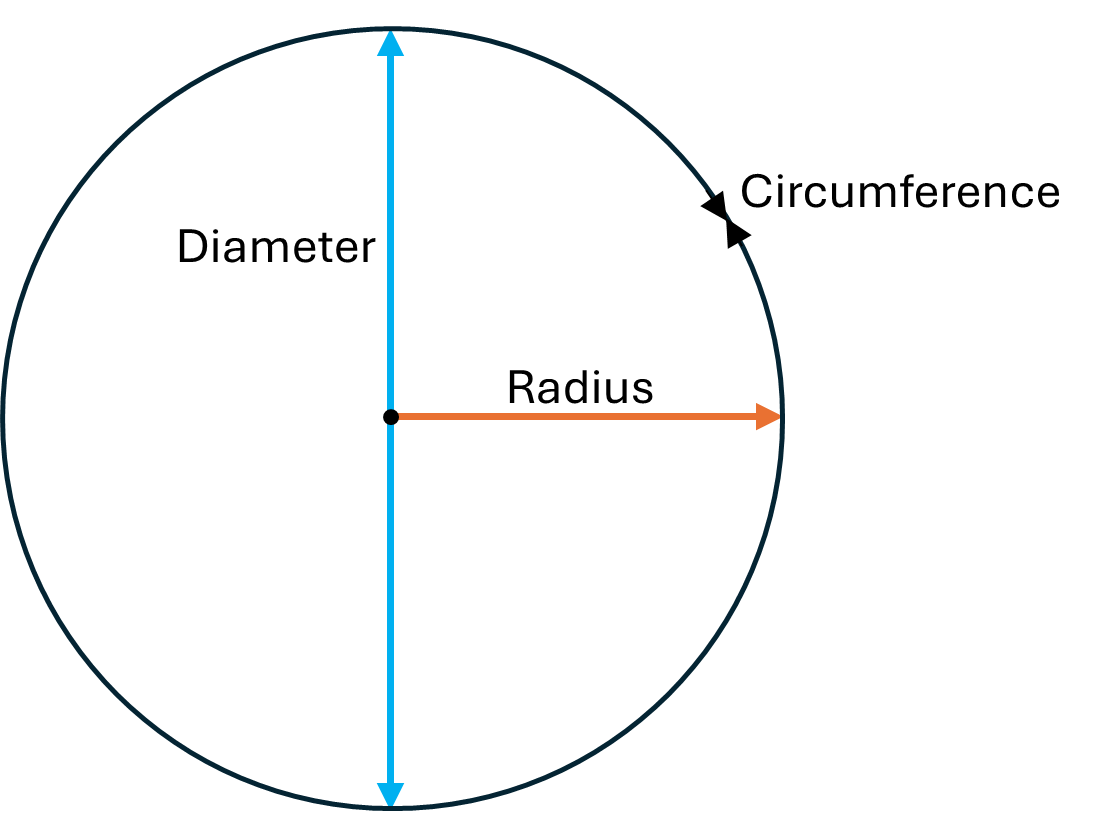
Example:

If a circle has a diameter of 34cm, calculate it’s circumference to two decimal places.

Solution:

\[\begin{aligned} C &= 2 \pi r \\\ &= 2 \times \pi \times 17 \\\ &= 106.81cm \\\ \end{aligned}\]

To find the arc length of a sector we use:

\[Arc\;length = \frac{\theta}{360} \times 2\pi r\]

So to find the perimeter of a sector we have:

\[Perimeter = \frac{\theta}{360} \times 2\pi r + 2r\]

Example:

Find the perimeter of the shape below. Give the answer to one decimal place.

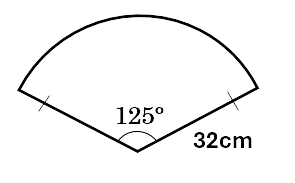
Solution:

\[\begin{aligned} &= \frac{\theta}{360} \times 2\pi r + 2r \\\ &= \frac{125}{360} \times 2 \times \pi \times 32 + 2 \times 32 \\\ &= 133.8cm \\\ \end{aligned}\]

To calculate the area of a triangle we use the formula:

\[Area = \frac{b \times h}{2}\]

which can also be written as:

\[Area = \frac{1}{2} b \times h\]

Where b is the value of the base of the triangle, and h is the height of the triangle.

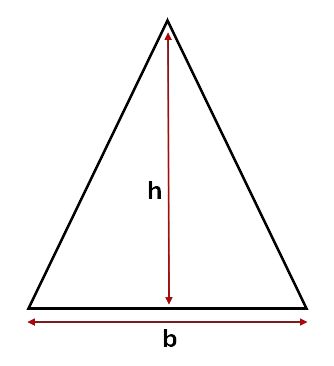
Example 1:

Calculate the area of the triangle.

Solution:

\[\begin{aligned} Area &= \frac{1}{2} b \times h \\\ &= \frac{1}{2} \times 18.2 \times 7 \\\ &= 63.7cm^2 \\\ \end{aligned}\]

Example 2:

Calculate the area of the triangle below.

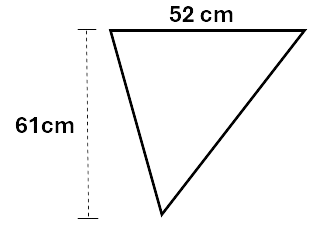
Solution:

\[\begin{aligned} Area &= \frac{b \times h}{2} \\\ &= \frac{52 \times 61}{2} \\\ &= 1\,586cm^2 \\\ \end{aligned}\]

For a rectangle we use:

\[Area = l \times w\]

Where l is the length of the rectangle, and w is the width.

Example:

Calculate the area of the rectangle.

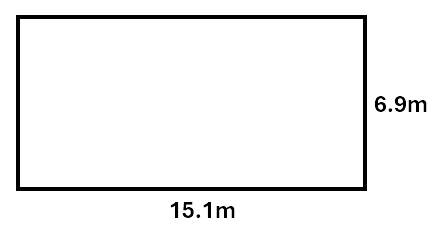
Solution:

\[\begin{aligned} Area &= l \times w \\\ &= 15.1 \times 6.9 \\\ &= 104.19m^2 \\\ \end{aligned}\]

A square is similar, however the length and the width is the same, so we use the formula:

\[Area = l^2\]

As l is the length on all sides.

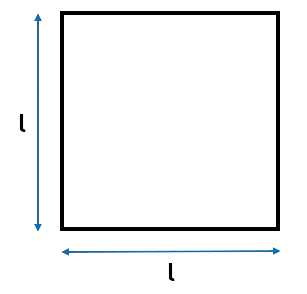
Example:

Calculate the area of a square with a length of \(6.5\,m\)

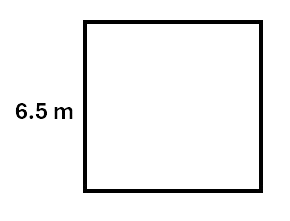
Solution:

\[\begin{aligned} Area &= l^2 \\\ &= 6.5^2 \\\ &= 42.25\,m^2 \\\ \end{aligned}\]

To find the area of a parallelogram we use:

\[Area = l \times h\]

Where l is the length of the shape, and h is the height.

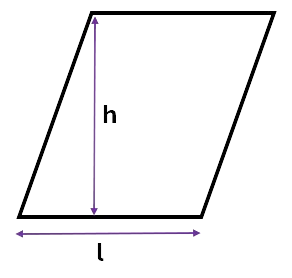
Example:

Calculate the area of the parallelogram.

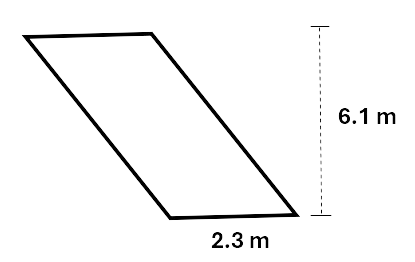
Solution:

\[\begin{aligned} Area &= l \times h \\\ &= 2.3 \times 6.1 \\\ &= 14.03\,m^2 \\\ \end{aligned}\]

For the area of a trapezium we use the formula:

\[Area = \frac{1}{2} (a + b) \times h\]

Where a is the length of the top side, b is the length of the bottom, and h is the height of the trapezium.

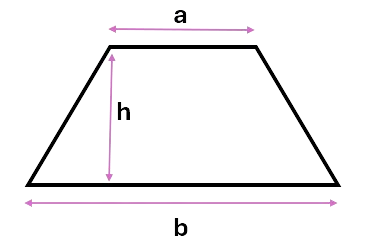
Example:

Calculate the area of the trapezium. Give the answer to one decimal place.

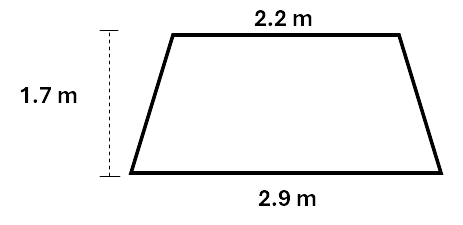
Solution:

\[\begin{aligned} Area &= \frac{1}{2} (a + b) \times h \\\ &= \frac{1}{2} (2.2 + 2.9) \times 1.7 \\\ &= 4.3 m^2 \\\ \end{aligned}\]

The area of a circle is calculated using the formula:

\[Area = \pi r^2\]

Where r is the radius of the circle.

Example:

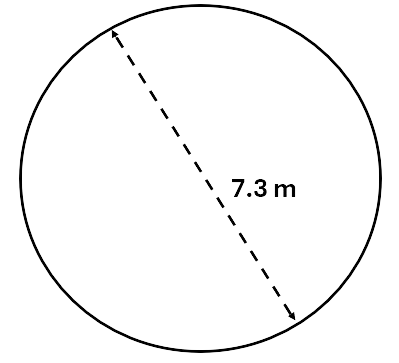
Calculate the area of a circle that \(7.3\,m\) wide to two decimal places.

Solution:

We know the diameter of the circle is \(7.3\,m\), so we first need to halve this to find the radius:

\[r = 7.3 \div 2 = 3.65\]

Therefore:

\[\begin{aligned} Area &= \pi\;r^2 \\\ &= \pi \times 3.65^2 \\\ &= 41.85\,m^2 \\\ \end{aligned}\]

We can also find the area of sectors within a circle using the formula:

\[Area = \pi r^2 \times \frac{\theta}{360}\]

Where r is again the radius of the circle, and \(\theta\) is the angle of the sector.

Example:

Calculate the area of the shape below. Give the answer to one decimal place.

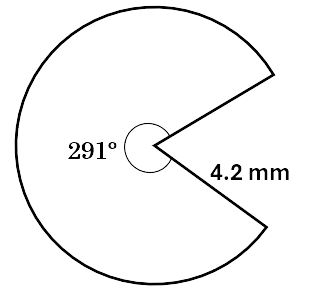
Solution:

\[\begin{aligned} Area &= \pi r^2 \times \frac{\theta}{360} \\\ &= \pi \times 4.2^2 \times \frac{291}{360} \\\ &= 44.8\,mm^2 \\\ \end{aligned}\]