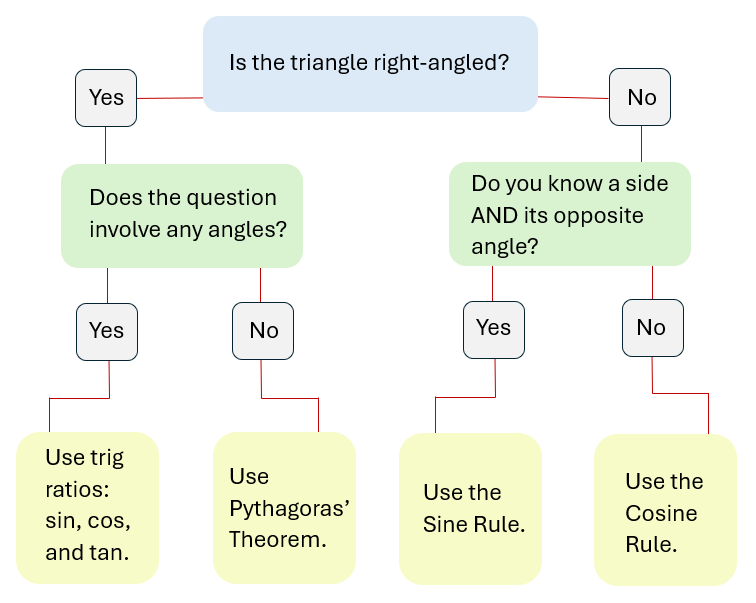
Geometry and trigonometry
Trigonometry is the study of triangles and their angles. This page covers key concepts within trigonometry including Pythagoras’ theorem, trigonometric ratios and the sine and cosine rules.
Triangles
A triangle is a figure that has three sides. Generally, the angles of a triangle are represented using capital letters, and the sides are represented by lower case letters. Side a will always be opposite angle A, side b will be opposite angle B, and side c will be opposite angle C.
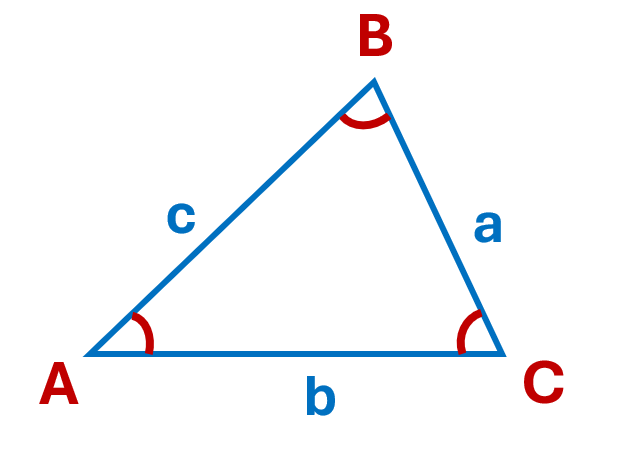
If the sides aren’t labelled, we can refer to them as AB, BC, and AC. The angles may also be referred to as \(\angle A\), \(\angle B\) and \(\angle C\). Each angle may also be referred to in relation to the labelled points of the triangle. For example, \(\angle A\) could also be \(\angle BAC\), \(\angle B\) could also be \(\angle ABC\), and \(\angle C\) can be written as \(\angle ACB\). If this is the case, notice the angle you are working with will always be at the letter in the middle.
The sum of the angles inside any triangle will always be \(180^\circ\).
There are six types of triangles:
Acute triangles contain angles that are each less than \(90^\circ\).
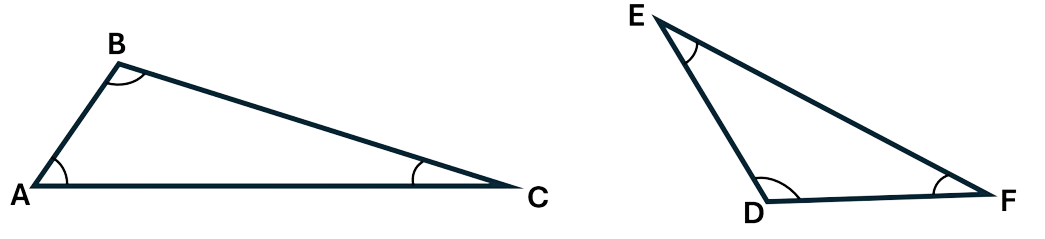
Obtuse triangles contain one angle that is more than \(90^\circ\). The other two angles will be acute angles. You can see in the below triangles that angles B and D are both more than \(90^\circ\), while A, C, E and F are all acute angles.
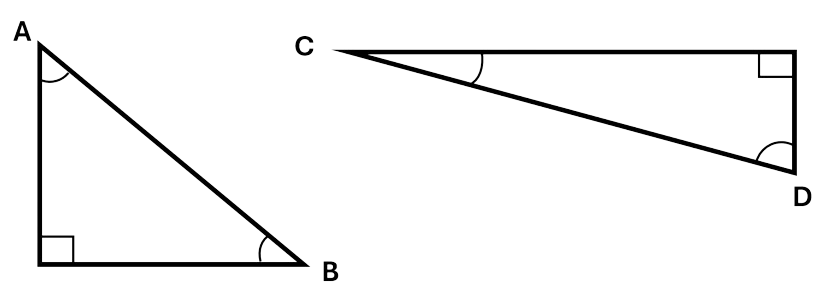
Right-angled triangles contain an angle that is equal to \(90^\circ\). This angle is usually marked by a little square in that corner.
All angles within an equilateral triangle are the same value, and all sides are the same length. As all angles within a triangle add up to \(180^\circ\), each angle in an equilateral triangle will be \(60^\circ\).
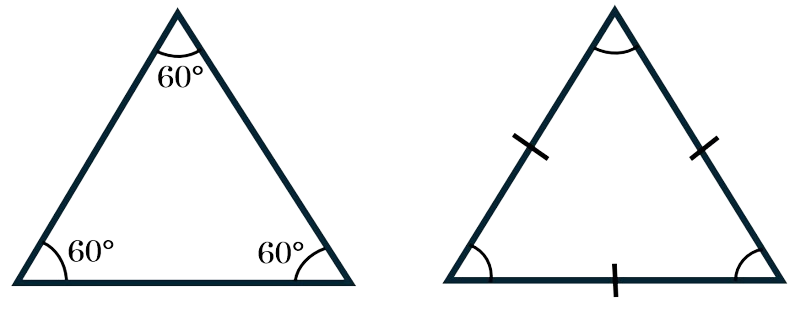
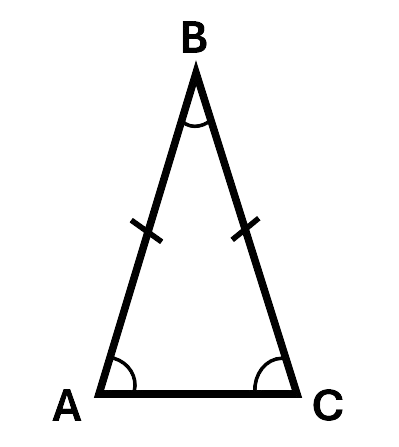
Isosceles triangles have two equal sides and two equal angles. The equal sides below are shown using lines on each matching side.
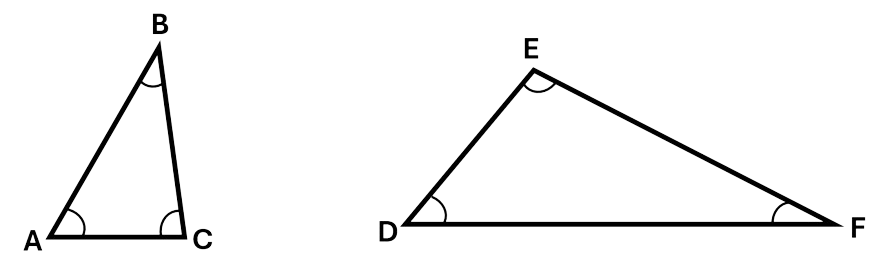
In scalene triangles all the angles are different sizes and all of the sides are different lengths. Acute, obtuse, and right-angled triangles can all be scalene triangles as well, as seen below. The triangle on the left is both a scalene triangle and an acute triangle, as all the angles are less than \(90^\circ\), while the triangle on the right is both scalene and obtuse as angle E is larger than \(90^\circ\).
Check your understanding of different types of triangles by working through the activity:
Pythagoras’ theorem
Pythagoras’ theorem shows us that the values of all the sides in a right-angled triangle are related. Given the triangle below:
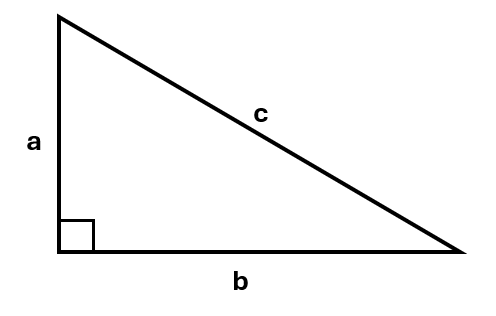
Pythagoras’ theorem tells us that:
\[a^2 + b^2 = c^2\]In the formula, the side c is always the hypotenuse.
If we know the values of two of the sides, we can use Pythagoras’ theorem to find the unknown third side.
Example 1: Given the triangle below, find the value of \(\chi\).
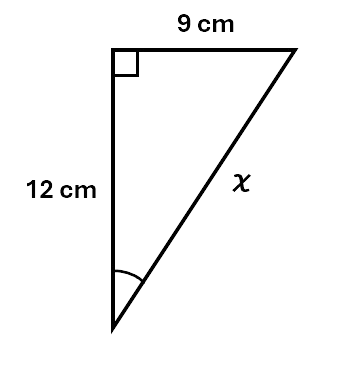
Solution:
\[\begin{aligned} a^2 + b^2 &= c^2 \\\ 9^2 + 12^2 &= \chi^2 \\\ 81 + 144 &= \chi^2 \\\ 225 &= \chi^2 \\\ \sqrt{225} &= \chi \\\ \chi &= 15cm \\\ \end{aligned}\]Example 2: Given the triangle below, find the value of y to 2 decimal places.
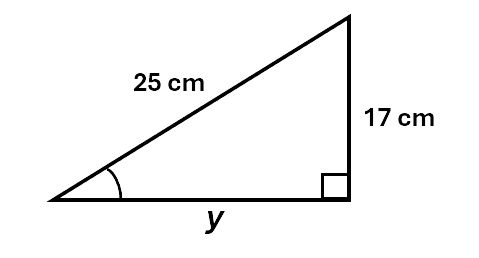
Solution:
\[\begin{aligned} a^2 + b^2 &= c^2 \\\ a^2 &= c^2 - b^2 \\\ y^2 &= 25^2 - 17^2 \\\ y^2 &= 336 \\\ y &= \sqrt{336} \\\ y &= 18.33cm \\\ \end{aligned}\]Note: We can rearrange our equations using algebra.
Check your understanding of Pythagoras’ theorem using the questions below.
Similar triangles
Two triangles are considered similar if they have the same shape, in terms of having the same angles. However, they don’t necessarily need to be the same size (if they are actually the same size, this is a special kind of similar triangle called a congruent triangle). To establish that two triangles are similar you need to show that one of the following criteria are met (as then the rest will follow):
- Two pairs of corresponding angles are equal
- Three pairs of corresponding sides are proportional
- Two pairs of corresponding sides are proportional and the corresponding angles between them are equal
You could think of similar triangles as either an enlargement or reduction of each other.
Example 1:
The two triangles below are similar as their corresponding sides are proportional (the sides of the smaller triangle are half the size of the larger triangle). You could rotate the triangle on the right to make it look the same as one on the left.
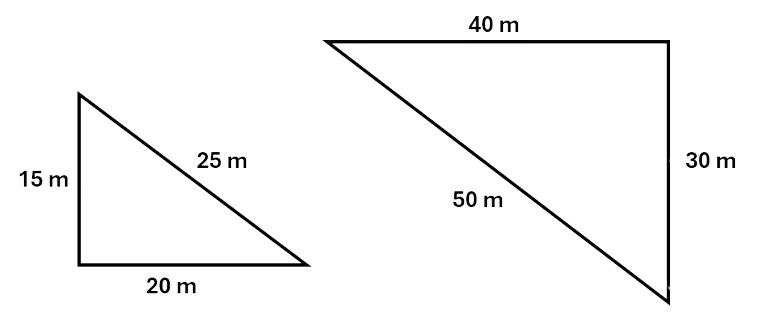
Example 2:
The two triangles below are similar triangles as their corresponding angles are equal in size. Both the large triangle and the smaller, purple, triangle share the \(\angle B\). In addition, as lines \(DE\) and \(AC\) are perpendicular, \(\angle A\) and \(\angle D\) are equal, and \(\angle C\) and \(\angle E\) are equal.
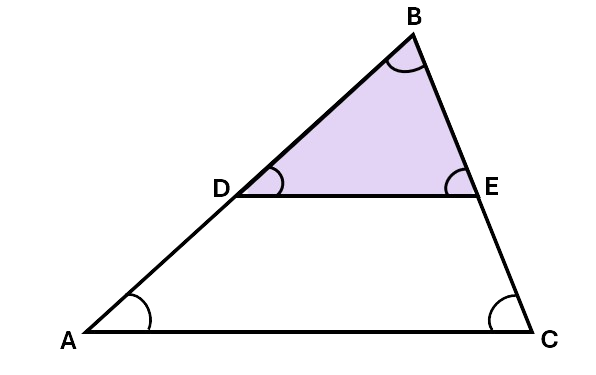
Example 3:
Given the two triangles below are similar, find the value of lines \(JL\) and \(KL\).
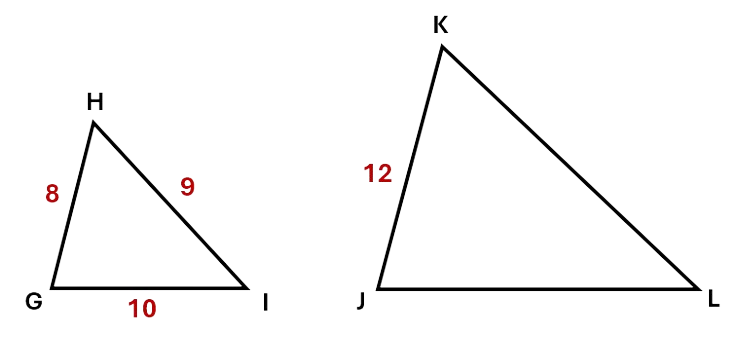
Solution:
To find line \(JL\):
\[\begin{aligned} \frac{GH}{JK} &= \frac{GI}{JL} \\\ \frac{8}{12} &= \frac{10}{JL} \\\ 8 \times JL &= 120 \\\ JL &= 15 \\\ \end{aligned}\]To find \(KL\):
\[\begin{aligned} \frac{GH}{JK} &= \frac{HI}{KL} \\\ \frac{8}{12} &= \frac{9}{KL} \\\ 8 \times KL &= 108 \\\ JL &= 13.5 \\\ \end{aligned}\]Note: We can rearrange our equations using algebra.
You can check your understanding of similar triangles by working through the questions below.
Trigonometric ratios
There are six trigonometric functions that we can use to show us the relationship between the acute angles in a right-angled triangle and the length of its sides. You are likely to only need to use three of these functions. They are:
- Sine (\(\sin\))
- Cosine (\(\cos\))
- Tangent (\(\tan\))
While using trigonometric functions, the angle you are using in the right-angled triangle is represented by the symbol \(\theta\), known as theta.
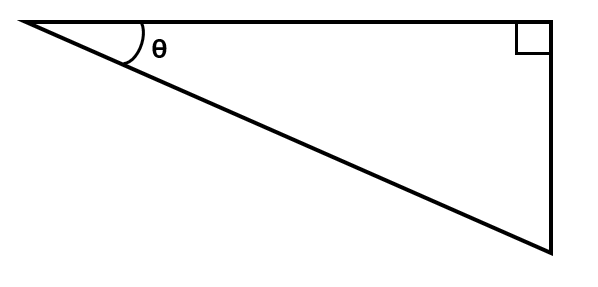
Each side of the right-angled triangle has a name. The longest side, that is always opposite the right angle, is known as the hypotenuse. The other two sides are called the opposite and the adjacent sides. The opposite side is always the side that sits opposite the angle we are using in our calculation. The adjacent side is the side that sits next to the angle, along with the hypotenuse.
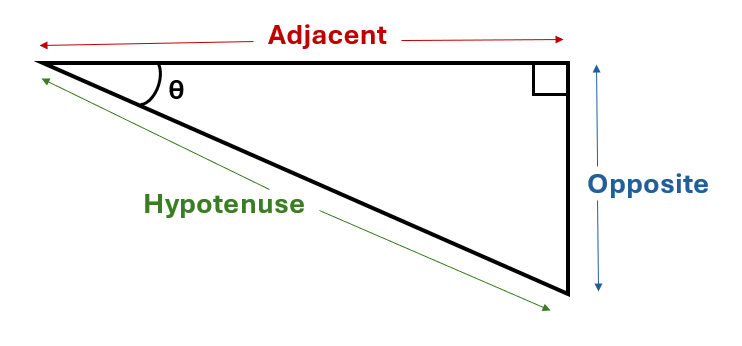
We can use trigonometric functions to calculate the trigonometric ratios of an angle with respect to the sides of a right-angled triangle. To find the sine ratio of the angle, we divide the value of the side opposite to the angle by the value of the hypotenuse. To find the cosine ratio of the angle, we divide the value of the adjacent side to the angle by the hypotenuse. To find the tangent ratio of the angle, we divide the value of the side opposite the angle by the side adjacent to the angle.
These rules are written:
\[\sin\theta = \frac{opp}{hyp}\] \[\cos\theta = \frac{adj}{hyp}\] \[\tan\theta = \frac{opp}{adj}\]You can use the acronym SOHCAHTOA to help you remember which sides are used with each function:

Example: Given the triangle below, find the values of angles B and C to two decimal places.
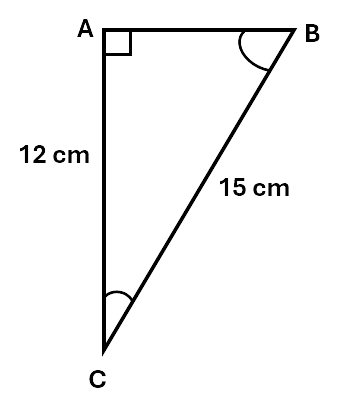
Solution: For \(\angle B\):
First, work out which side is the opposite and which is the adjacent. The longest side, opposite the right angle, is always the hypotenuse.
Side AC is opposite angle B. Side AB is adjacent. The hypotenuse is BC. We don’t know the value of AB, so we’re going to use the sine function.
\[\sin\theta = \frac{opp}{hyp}\] \[\sin B = \frac{12}{15}\] \[\sin B = 0.8\]We can then use the inverse sine function on a calculator (sometimes called arc sine) to find the angle whose sine is equal to \(0.8\):
\[\begin{aligned} B &=\sin^{-1} 0.8 \\\ B &= 53.13^\circ \\\ \end{aligned}\]We can now find \(\angle C\) in two different ways:
One way is by using a trigonometric function. This time, AC is the adjacent side. As we know the values of the adjacent and hypotenuse, we’re going to use the cos function.
\[\begin{aligned} \cos\theta &= \frac{adj}{hyp} \\\ \cos C &= 0.8 \\\ C &= \cos^{-1} 0.8 \\\ C &= 36.87^\circ \\\ \end{aligned}\]Another way to find \(\angle C\) is by using the fact that all angles in any triangle add up to \(180^\circ\).
\[180 - 90 - 53.13 = 36.87^\circ\]Check your understanding of how to use trigonometric ratios by working through the questions below.
Sine rule
The sine rule can be used in any triangle where a side and its opposite angle are known.
When we’re given a triangle, for example:
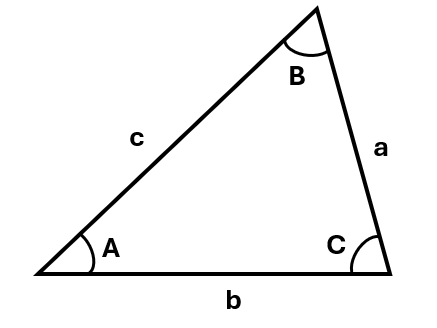
We can find the value of a side of a triangle using the sine rule:
\[\frac{a}{sin\;A} = \frac{b}{sin\;B} = \frac{c}{sin\;C}\]To find the value of an angle, rearrange the sine rule so that the angles are on the top:
\[\frac{sin\;A}{a} = \frac{sin\;B}{b} = \frac{sin\;C}{c}\]To use the sine rule you will need to know at least one pair of a side with its opposite angle, and you will only need to use two parts of the sine rule, not all three.
Example 1: Find the value of K to two decimal places.

Solution:
\[\begin{aligned} \frac{a}{sin\;A} &= \frac{b}{sin\;B} \\\ \frac{K}{sin\;50^\circ} &= \frac{21}{sin\;85^\circ} \\\ K &= \frac{21\,sin\;50^\circ}{sin\;85^\circ} \\\ K &= 16.15cm \\\ \end{aligned}\]Example 2: Find the value of \(\angle \theta\) to two decimal places.
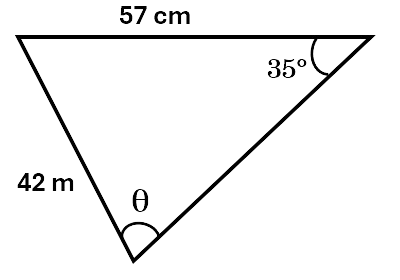
Solution:
\[\begin{aligned} \frac{sin\;A}{a} &= \frac{sin\;B}{b} \\\ \frac{sin\;\theta}{57} &= \frac{sin\;35^\circ}{42} \\\ sin\;\theta &= \frac{57\,sin\;35^\circ}{42} \\\ sin\;\theta &= 0.778425 \\\ sin^{-1} 0.778425 &= 51.116 \\\ \theta &= 51.12^\circ \\\ \end{aligned}\]Check your understanding of the sine rule by working through the questions below.
Cosine rule
The cosine rule is used in any triangle when relating all three sides to one angle. Consider the triangle below:
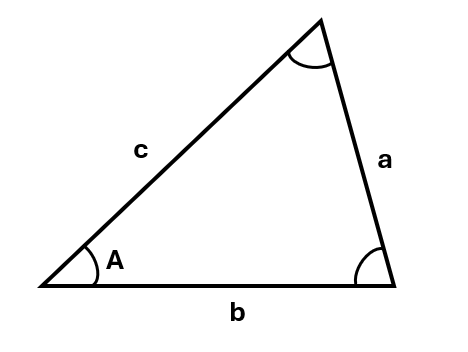
The cosine rule tells us:
\(a^2 = b^2 + c^2 - 2bc\) \(cos\;A\)
To find the value of the angle rather than the value of a side, we can rearrange the formula:
\[cos\;A = \frac{b^2 + c^2 - a^2}{2bc}\]Remember that the \(\angle A\) will always be opposite side a.
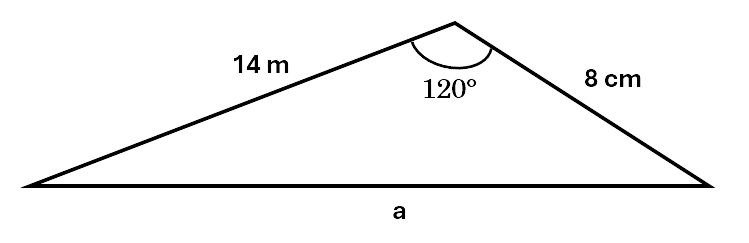
Example 1: Find the value of a, to one decimal place.
Solution:
\[\begin{aligned} a^2 &= b^2 + c^2 - 2bc\;cos\;A \\\ a^2 &= 8^2 + 14^2 - 2 \times 8 \times 14cos\;120^\circ \\\ a^2 &= 64 + 196 - 224 \times (-0.5) \\\ a^2 &= 372 \\\ a &= \sqrt 372 \\\ a &= 19.3 m \\\ \end{aligned}\]Example 2: Find the value of \(\angle \theta\) to two decimal places.
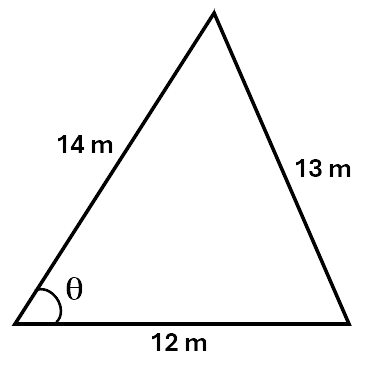
Solution:
\[\begin{aligned} cos\;A &= \frac{b^2 + c^2 - a^2}{2bc} \\\ cos\;\theta &= \frac{12^2 + 14^2 - 13^2}{2 \times 12 \times 14} \\\ cos\;\theta &= \frac{12^2 + 14^2 - 13^2}{2 \times 12 \times 14} \\\ cos\;\theta &= \frac{171}{336} \\\ cos\;\theta &= 0.50893 \\\ \theta &= cos^{-1}\,0.50893 \\\ \theta &= 59.41^\circ \\\ \end{aligned}\]Check your understanding by working through the questions below.
What formula should I use?