Geometry and trigonometry
This page explains how to calculate the perimeter and area of two-dimensional shapes.
In brief, it covers the following:
- The definition of perimeter, and how to calculate this for polygons
- The definition of circumference, and how to calculate this as well as the perimeter of circle sectors
- The definition of area, and how to calculate this for some common polygons as well as for circles and sectors
Perimeter
Perimeter is the distance around any two-dimensional shape. In this section we will focus on the perimeter of polygons, while the perimeter of circles is covered in the Circumference section.
To calculate the perimeter of a polygon we simply add together the values of the various sides.
Example:
Calculate the perimeter of the shape below.

Solution:
To calculate the perimeter we need to add up the value of each side. To do this for the shape above, we first need to determine the values of the three sides that are not labelled.
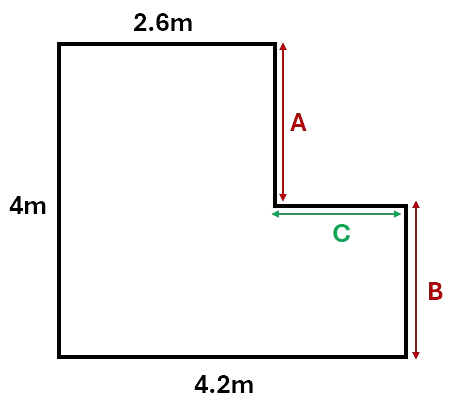
From the image above, we can see that sides A and B together will give us another \(4m\). We can find side C by subtracting \(2.6\) from \(4.2\), therefore C is \(1.6m\).
So the perimeter of the shape will be:
\[P = 2.6 + 4 + 4.2 + 4 + 1.6 = 16.4m\]Check your understanding of perimeter by working through the questions below.
Polygons with two perimeters
Sometimes you will encounter polygons with both an internal and an external perimeter, such as the external walls or concrete footings of a building:

To find one perimeter given the other you need to know the thickness of the wall or footing. For example, to find the external perimeter we will need to know the thickness measurement as well as the internal perimeter, and to find the internal perimeter we will need to know the thickness measurement as well as the external perimeter.
The two perimeters of a shape will be:
\[\begin{aligned} External\;perimeter &= internal\;perimeter\;+ \\\ & 2 \times the\;wall\;thickness \times the\;number\;of\;corners \\\ \end{aligned}\] \[\begin{aligned} Internal\;perimeter &= external\;perimeter\;- \\\ & 2 \times the\;wall\;thickness \times the\;number\;of\;corners \\\ \end{aligned}\]You may also need to find the average of the two perimeters, or the mean girth. How you do this will depend on the information you have.
If you know the values of both the external and internal perimeters:
\(Mean\;girth = (external\;perimeter + internal\;perimeter) \div 2\)
If you know the thickness of the wall and the external perimeter:
\[\begin{aligned} Mean\;girth &= external\;perimeter\;-\\\ & the\;wall\;thickness \times the\;number\;of\;corners \\\ \end{aligned}\]If you know the thickness of the wall and the internal perimeter:
\[\begin{aligned} Mean\;girth &= internal\;perimeter\;+\\\ & the\;wall\;thickness \times the\;number\;of\;corners \\\ \end{aligned}\]Example 1:
A rectangular brick wall has thickness \(120\,mm\) and internal perimeter \(48\,m\). Calculate the external perimeter.
Solution:
\[\begin{aligned} 120\,mm &= 0.12\,m \\\ External\;perimeter &= internal\;perimeter\;+ \\\ & 2 \times the\;wall\;thickness \times the\;number\;of\;corners \\\ &= 48 + 2 \times 0.12 \times 4 \\\ &= 48.96\,m \\\ \end{aligned}\]Example 2:
A square room has an external perimeter of \(33.4\,m\) and a thickness of \(0.18\,m\). Calculate the mean girth of the perimeters of this room.
Solution:
\[\begin{aligned} Mean\;girth &= external\;perimeter\;- \\\ & the\;wall\;thickness \times the\;number\;of\;corners \\\ &= 33.4 - 0.18 \times 4 \\\ &= 32.68\,m \\\ \end{aligned}\]Check your understanding of two perimeter polygons by working through the following questions.
Circumference
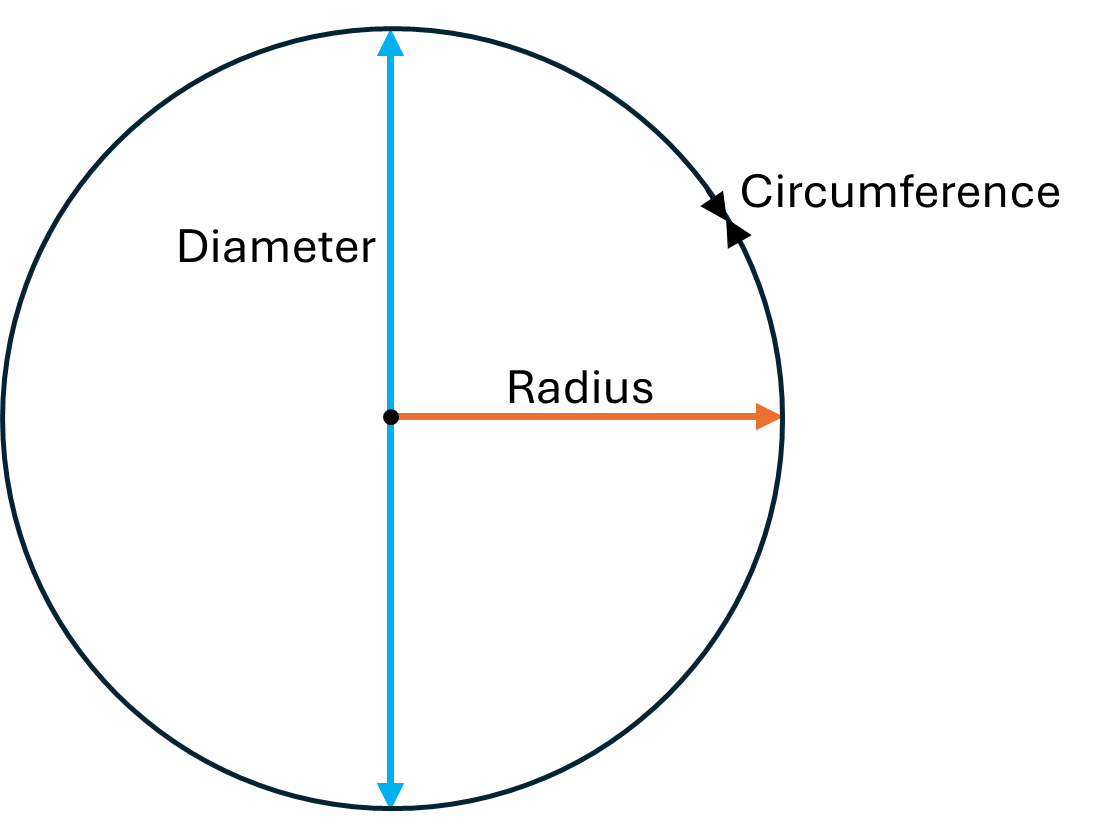
The perimeter of a circle is called the circumference of the circle.
We can calculate the circumference of a circle using the formula:
\[C = 2 \pi r\]Where \(r\) is the radius, or half the diameter, of the circle.
Example:
If a circle has a diameter of 34cm, calculate it’s circumference to two decimal places.
Solution:

Check your understanding of circumference by working through these questions.
Sectors
We can also find the perimeter of a sector of a circle. To do this we need to find the length of the arc and then add the two radii that form the sides of the sector.
To find the arc length of a sector we use:
\[Arc\;length = \frac{\theta}{360} \times 2\pi r\]So to find the perimeter of a sector we have:
\[Perimeter = \frac{\theta}{360} \times 2\pi r + 2r\]
Example:
Find the perimeter of the shape below. Give the answer to one decimal place.
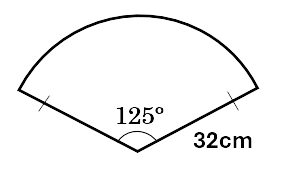
Solution:
\[\begin{aligned} &= \frac{\theta}{360} \times 2\pi r + 2r \\\ &= \frac{125}{360} \times 2 \times \pi \times 32 + 2 \times 32 \\\ &= 133.8cm \\\ \end{aligned}\]Check your understanding of sector perimeters by working through the questions below.
Area
The area of a two-dimensional shape is how much space it takes up on a surface. It is measured in \(m^2\) (as the base unit of measurement; other derived units of measurement such as \(cm^2\) or \(mm^2\) may also be used as appropriate). The formula used to calculate the area of a shape will depend on the type of shape in question.
Triangles
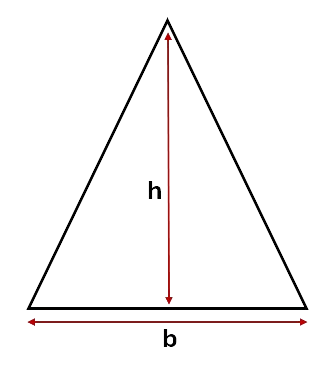
To calculate the area of a triangle we use the formula:
\[Area = \frac{b \times h}{2}\]which can also be written as:
\[Area = \frac{1}{2} b \times h\]Where b is the value of the base of the triangle, and h is the height of the triangle.
Example 1:
Calculate the area of the triangle.

Solution:
\[\begin{aligned} Area &= \frac{1}{2} b \times h \\\ &= \frac{1}{2} \times 18.2 \times 7 \\\ &= 63.7cm^2 \\\ \end{aligned}\]Example 2:
Calculate the area of the triangle below.
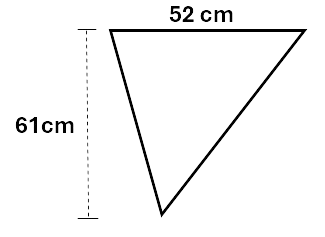
Solution:
\[\begin{aligned} Area &= \frac{b \times h}{2} \\\ &= \frac{52 \times 61}{2} \\\ &= 1\,586cm^2 \\\ \end{aligned}\]Check your understanding of the area of triangles by working through the questions below.
Quadrilaterals
A quadrilateral is any shape with four sides. However, not all quadrilaterals use the same formula for area.
For a rectangle we use:
\[Area = l \times w\]Where l is the length of the rectangle, and w is the width.

Example:
Calculate the area of the rectangle.
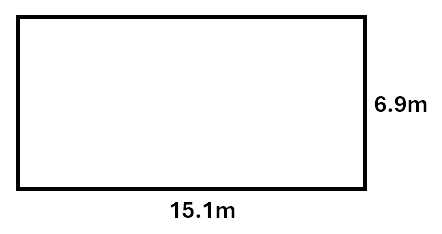
Solution:
\[\begin{aligned} Area &= l \times w \\\ &= 15.1 \times 6.9 \\\ &= 104.19m^2 \\\ \end{aligned}\]A square is similar, however the length and the width is the same, so we use the formula:
\[Area = l^2\]As l is the length on all sides.
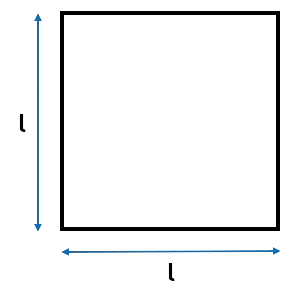
Example:
Calculate the area of a square with a length of \(6.5\,m\)
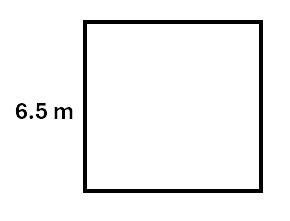
Solution:
\[\begin{aligned} Area &= l^2 \\\ &= 6.5^2 \\\ &= 42.25\,m^2 \\\ \end{aligned}\]To find the area of a parallelogram we use:
\[Area = l \times h\]Where l is the length of the shape, and h is the height.
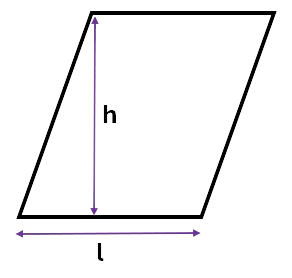
Example:
Calculate the area of the parallelogram.
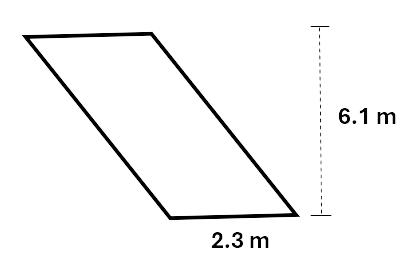
Solution:
\[\begin{aligned} Area &= l \times h \\\ &= 2.3 \times 6.1 \\\ &= 14.03\,m^2 \\\ \end{aligned}\]For the area of a trapezium we use the formula:
\[Area = \frac{1}{2} (a + b) \times h\]Where a is the length of the top side, b is the length of the bottom, and h is the height of the trapezium.
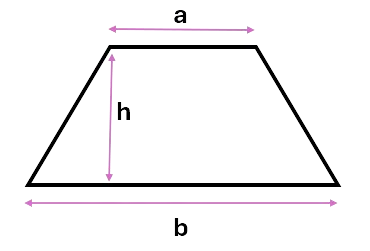
Example:
Calculate the area of the trapezium. Give the answer to one decimal place.
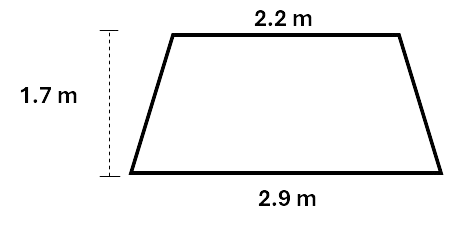
Solution:
\[\begin{aligned} Area &= \frac{1}{2} (a + b) \times h \\\ &= \frac{1}{2} (2.2 + 2.9) \times 1.7 \\\ &= 4.3 m^2 \\\ \end{aligned}\]Check your knowledge of the area of quadrilaterals by working though the following questions.
Circles
The area of a circle is calculated using the formula:
\[Area = \pi r^2\]Where r is the radius of the circle.

Example:
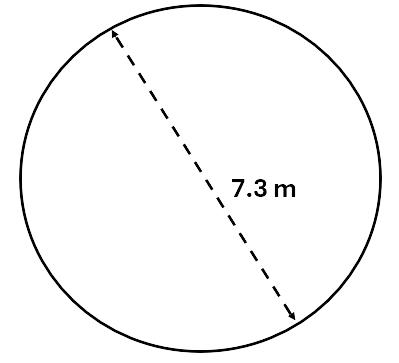
Calculate the area of a circle that \(7.3\,m\) wide to two decimal places.
Solution:
We know the diameter of the circle is \(7.3\,m\), so we first need to halve this to find the radius:
\[r = 7.3 \div 2 = 3.65\]Therefore:
\[\begin{aligned} Area &= \pi\;r^2 \\\ &= \pi \times 3.65^2 \\\ &= 41.85\,m^2 \\\ \end{aligned}\]Sectors
We can also find the area of sectors within a circle using the formula:
\[Area = \pi r^2 \times \frac{\theta}{360}\]Where r is again the radius of the circle, and \(\theta\) is the angle of the sector.
Example:
Calculate the area of the shape below. Give the answer to one decimal place.
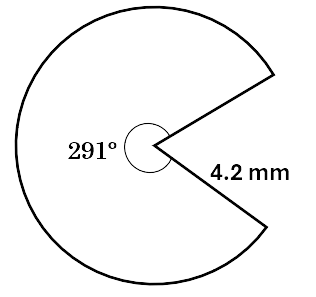
Solution:
\[\begin{aligned} Area &= \pi r^2 \times \frac{\theta}{360} \\\ &= \pi \times 4.2^2 \times \frac{291}{360} \\\ &= 44.8\,mm^2 \\\ \end{aligned}\]Check your knowledge of the area of circles and sectors by working through the following questions.