Geometry and trigonometry
Surface area
The surface area of a three-dimensional shape is the total area of its surface. It is measured in \(m^2\) (as the base unit of measurement; other derived units of measurement such as \(mm^2\) may also be used as appropriate). The formula used to calculate the surface area of a shape will depend on the type of shape in question, as demonstrated in the following sections.
Cubes
The surface area of a cube is equal to six times the area of one square side, as shown in the following formula.
Formula for a cube:
\[Surface\textrm{ }area = 6s^2\]Where \(s\) is the length of one side.
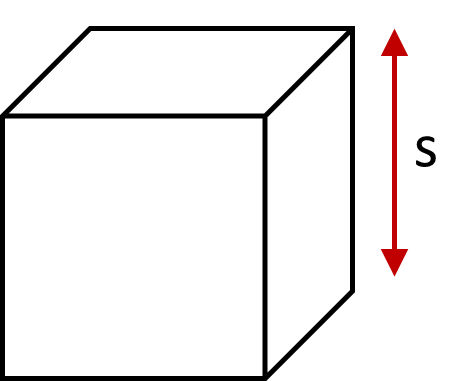
Example: Calculate the surface area of a cubic concrete block with side length \(300mm\)
Solution: Using the formula for surface area with this measurement gives:
\[Surface\textrm{ }area = 6 \times 300^2 = 540 000mm^2\]It would then be better to convert this to \(m^2\), as follows:
\[540 000 \div 1000^2 = 0.54m^2\]Alternatively, you could convert \(300mm\) to \(0.3m\) first and then calculate the surface area using that measurement to give the same result.
Check your understanding of how to calculate the surface area of cubes by completing the following activity:
Prisms
The surface area of a closed prism is calculated by adding together the area of the bases and the area of the sides, which can be done in different ways depending on the type of prism. This section covers one general formula that can be used for all closed prisms, along with specific formulas for calculating the surface area of triangular and rectangular prisms.
Formula for any closed prism:
\[Surface\textrm{ }area = 2A + (h \times p)\]Where \(A\) is the area of the base, \(p\) is the perimeter of the base and \(h\) is the height of the prism.
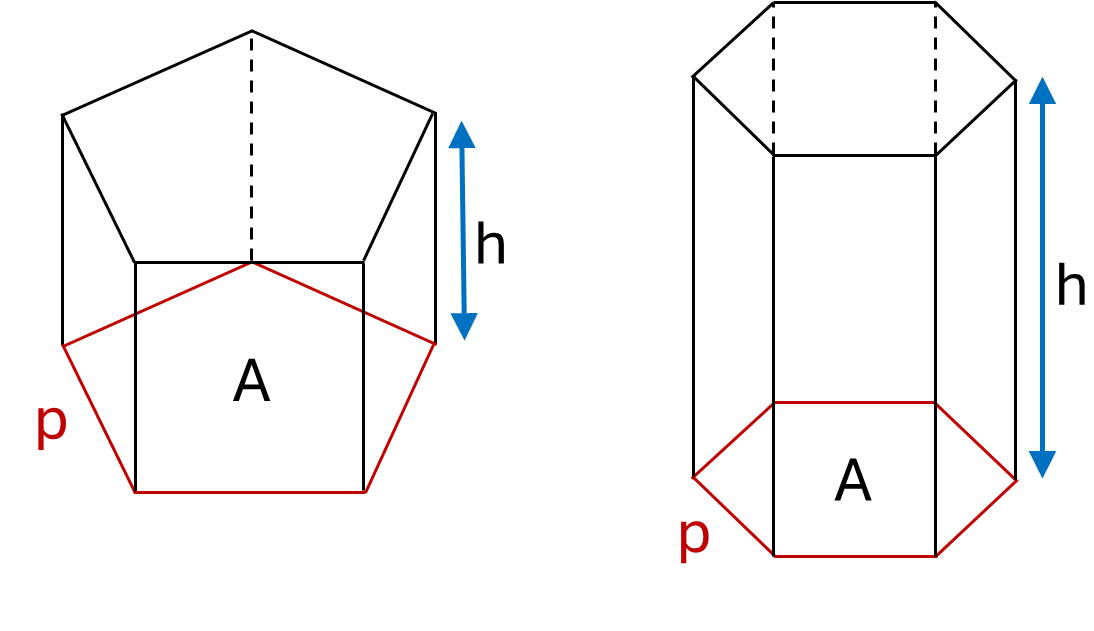
Example: Calculate the surface area of a hexagonal prism column with base area \(0.1m^2\), base perimeter \(1.2m\) and height \(3m\).
Solution: Using the formula for surface area with these measurements gives:
\[Surface\textrm{ }area = 2 \times 0.1 + (3 \times 1.2) = 3.8m^2\]\(\)
When the prism is a triangular prism you may wish to use a specific formula instead. This formula adds together the area of the triangular bases and the area of the three rectangular lateral faces (two of which are the same size).
Formula for a triangular prism:
\[Surface\textrm{ }area = bh + 2ls + lb\]Where \(b\), \(h\) and \(s\) are the base, height and side length of the triangles respectively, and \(l\) is the length of the prism.
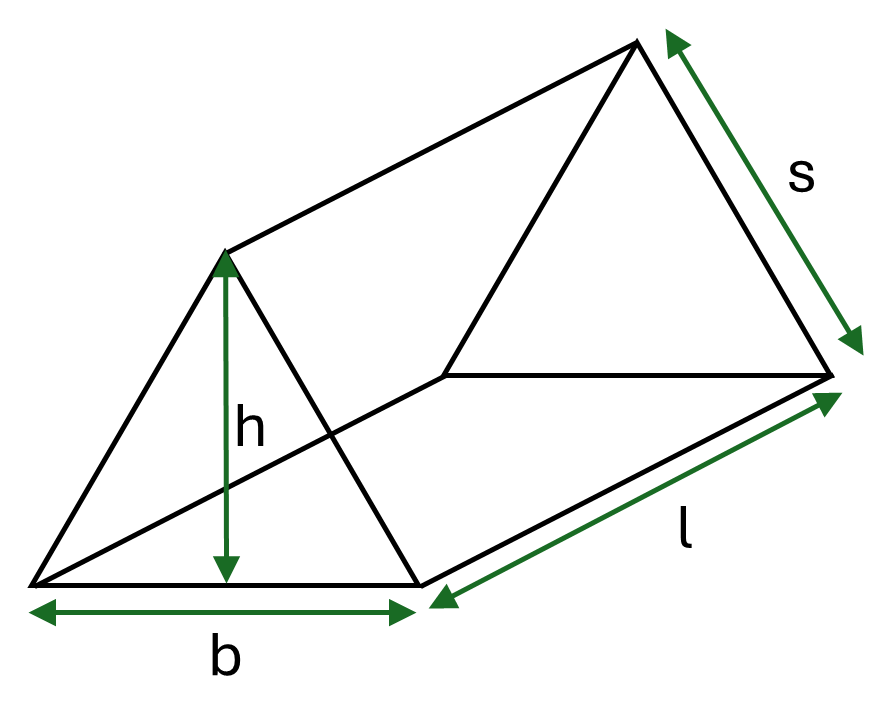
Example: Calculate the surface area of a timber triangular prism which has triangles with base \(63.6mm\), height \(31.8mm\) and side length \(45mm\) and which has length \(2.5m\).
Solution: First we should convert all the units to the same measurement. We will give our final answer in \(m^2\), so we will convert all measurements to \(m\) (although note that you could convert the one measurement that is in \(m\) to \(mm\) here and then convert to \(m^2\) at the end instead if preferred).
\[b = 63.6 \div 1000 = 0.0636m\] \[h = 31.8 \div 1000 = 0.0318m\] \[s = 45 \div 1000 = 0.045m\]We can then use these measurements in the formula to give the following:
\[Surface\textrm{ }area = 0.0636 \times 0.0318 + 2 \times 2.5 \times 0.045 + 2.5 \times 0.0636 = 0.386m^2\]\(\)
Similarly, when the prism is a rectangular prism you may wish to use a specific formula instead of the general formula.
This formula adds together the area of each pair of rectangular sides (one pair of bases and two pairs of lateral faces).
Formula for a rectangular prism:
\[Surface\textrm{ }area = 2lh + 2lw + 2wh\]Where \(l\) is the length of the prism, \(w\) is the width and \(h\) is the height.
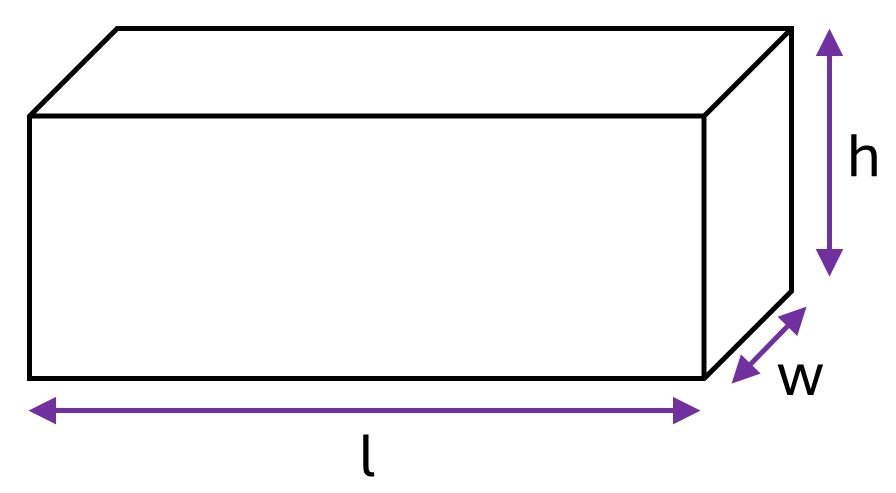
Example: Calculate the surface area of a timber rectangular prism which is \(1.2m\) long, \(0.03m\) wide and \(0.05m\) high.
Solution: Using the formula with these measurements gives:
\[Surface\textrm{ }area = 2 \times 1.2 \times 0.05 + 2 \times 1.2 \times 0.03 + 2 \times 0.03 \times 0.05 = 0.195m^2\]Check your understanding of how to calculate the surface area of prisms by completing the following activity:
Pyramids
Formulas to calculate the surface area of regular tetrahedrons and square pyramids are covered in this section. Note that the formula for the regular tetrahedron can be derived using Pythagoras’ theorem, which shows that the area of an equilateral triangle with side length \(b\) is \(\frac{\sqrt{3}}{4}b^2\)
Formula for a regular tetrahedron:
\[Surface\textrm{ }area = \sqrt 3 b^2\]Where \(b\) is the length of the sides of the equilateral triangles.
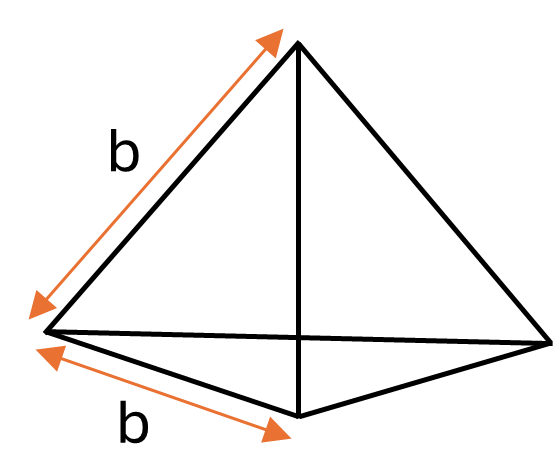
Example: Calculate the surface area of a regular tetrahedron with side length \(0.6m\)
Solution: Using the formula with this measurement gives:
\[Surface\textrm{ }area = \sqrt{3} \times 0.6^2 = 0.624m^2\]\(\)
If you have a square pyramid instead, the surface area is the sum of the area of the square base and the area of the four sides, as shown in the following formula.
Formula for a square pyramid:
\[Surface\textrm{ }area = s^2 + 2sl\]Where \(s\) is the length of the sides of the square and \(l\) is the slant height of the sides of the pyramid.
Alternatively, if you don’t know the slant height of the sides but know the perpendicular height of the pyramid you can use the following formula (which makes use of Pythagoras’ theorem to derive the slant height):
\[Surface\textrm{ }area = s^2 + 2s\sqrt{\frac{s^2}{4}+h^2}\]Where \(s\) is the length of the sides of the square and \(h\) is the perpendicular height of the pyramid.
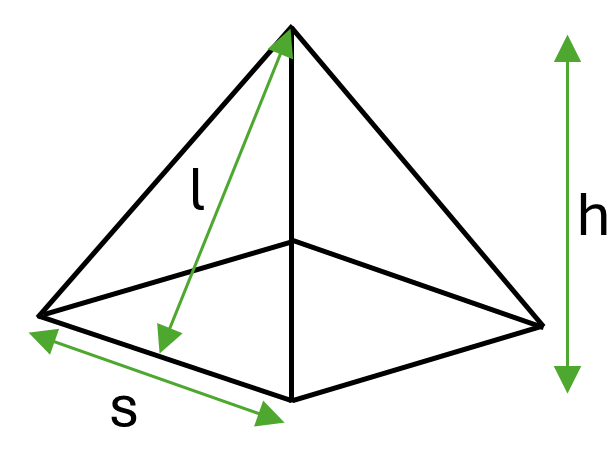
Example: Calculate the surface area of a square pyramid with square side length \(30mm\) and perpendicular height \(50mm\).
Solution: Using the formula with these measurements gives:
\[Surface\textrm{ }area = 30^2 + 2 \times 30 \times \sqrt{\frac{30^2}{4}+50^2} = 4032.09mm^2\]Check your understanding of how to calculate the surface area of pyramids by completing the following activity:
Cylinders
The surface area of a closed cylinder is equal to the area of the two circles on the ends, plus the area of the side. This side, when flattened out, is a rectangle with length equal to the circumference of the circles and width equal to the height of the cylinder. Therefore formulas for the circumference and area of circles are utilised in the formula for the surface area of a cylinder, as shown below.
Formula for a cylinder:
\[Surface\textrm{ }area = 2 \pi r^2 + 2 \pi rh\]Where \(r\) is the radius and \(h\) is the height of the cylinder. Note that you can also write this formula as \(2 \pi r (r + h)\)
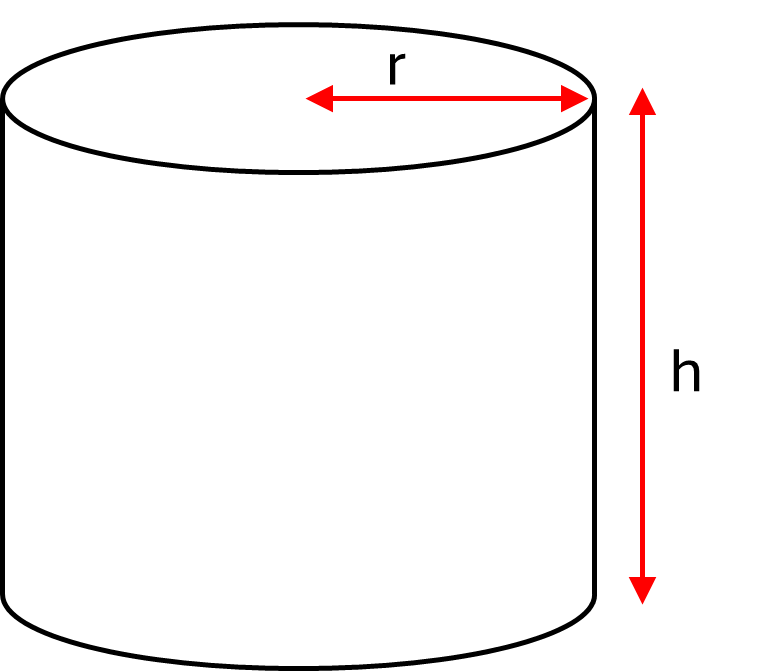
Example: Calculate the surface area of a cylindrical column with radius \(0.15m\) and height \(2.5m\)
Solution: Using the formula for surface area with these measurements gives:
\[Surface\textrm{ }area = 2 \times \pi \times 0.15^2 + 2 \times \pi \times 0.15 \times 2.5 = 2.498m^2\]Check your understanding of how to calculate the surface area of cylinders by completing the following activity:
Spheres
Archimedes proved that the surface area of a sphere is equal to the surface area of the open (at both ends) cylinder that fits perfectly around the sphere. In other words, the cylinder with radius equal to the radius of the sphere, and height equal to twice the radius of the sphere (i.e. to the diameter of the sphere).
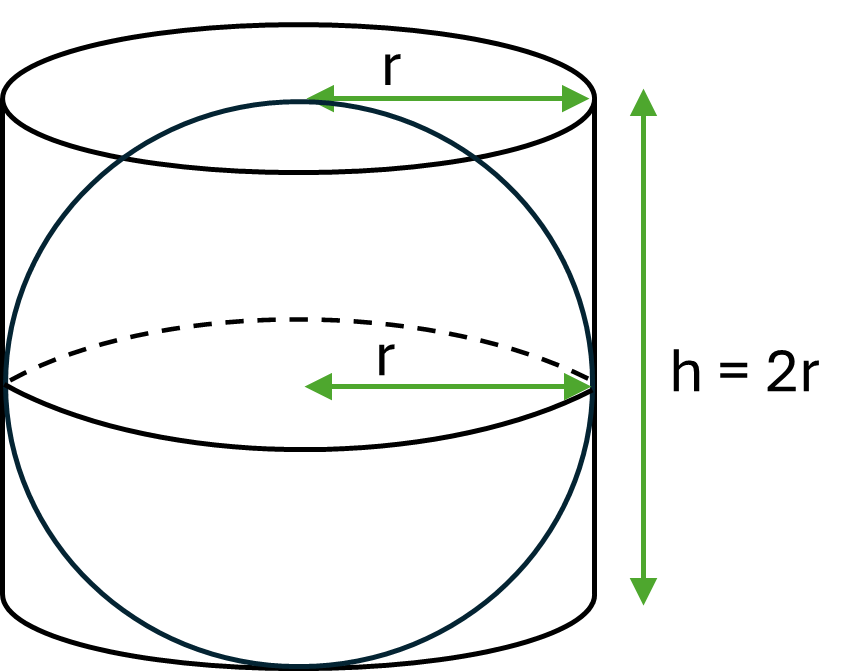
Therefore the formula for the surface area of a sphere is the same as the second part of the formula for the surface area of a cylinder (i.e. \(2 \pi rh\)), with \(2r\) substituted in for the height. This results in the simplified formula shown below.
Formula for a sphere:
\[Surface\textrm{ }area = 4 \pi r^2\]Where \(r\) is radius of the sphere.
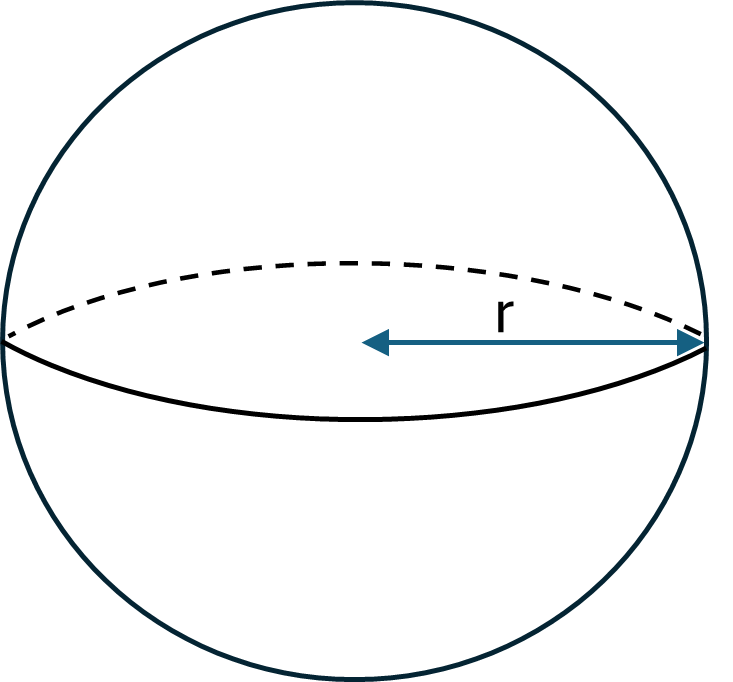
Example: Calculate the surface area of a sphere with diameter \(0.7m\)
Solution: First note that the radius of this sphere is \(0.35m\) (i.e. half the diameter). Using the formula for surface area with this measurement gives:
\[Surface\textrm{ }area = 4 \times \pi \times 0.35^2 = 1.539m^2\]Check your understanding of how to calculate the surface area of spheres by completing the following activity:
Cones
The surface area of a cone is equal to the area of the circular base plus the area of the curved surface, the latter of which can be calculated by thinking of it as being opened out to form a sector. Formulas for the area and arc length of sectors can therefore be used to derive the following formula for the surface area of a cone.
Formula for a cone:
\[Surface\textrm{ }area = \pi r^2 + \pi rs\]Where \(r\) is the radius of the base of the cone and \(s\) is the slant height. Note that you can also write this formula as \(\pi r (r + s)\)
Alternatively, if you don’t know the slant height but know the perpendicular height of the cone you can use the following formula (which makes us of Pythagoras’ theorem to derive the slant height):
\[Surface\textrm{ }area = \pi r^2 + \pi r \sqrt{h^2 + r^2}\]Where \(r\) is the radius of the base of the cone and \(h\) is the perpendicular height. Note that you can also write this formula as \(\pi r (r + \sqrt{h^2 + r^2})\)
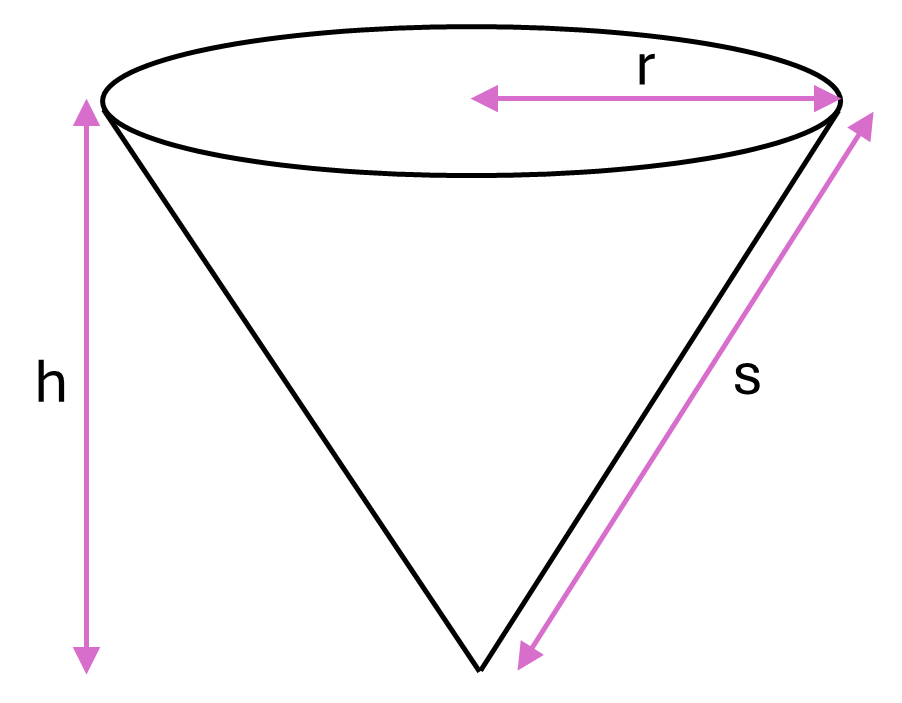
Example: Calculate the surface area of a cone with perpendicular height \(0.7m\) and base diameter \(0.3m\)
Solution: First note that the radius of the base of this cone is \(0.15m\) (i.e. half the diameter). Using the formula for surface area with this measurement gives:
\[Surface\textrm{ }area = \pi \times 0.15^2 + \pi \times 0.15 \times \sqrt{0.7^2 + 0.15^2} = 0.408m^2\]Check your understanding of how to calculate the surface area of cones by completing the following activity:
Volume
The volume of a three-dimensional shape is the amount of space it takes up. It is measured in \(m^3\) (as the base unit of measurement; other derived units of measurement such as \(mm^3\) may also be used as appropriate). The formula used to calculate the volume of a shape will depend on the type of shape in question, as demonstrated in the following sections.
Cubes
The volume of a cube can be calculated by multiplying the length by the width and height. Since these are all the same this equates to raising the length of one side to the power of three, as shown in the following formula.
Formula for a cube:
\[Volume = s^3\]Where \(s\) is the length of one side.
Example: Calculate the volume of a cubic concrete block with side length \(300mm\)
Solution: Using the formula for volume with this measurement gives:
\[Volume = 300^3 = 27 000 000mm^3\]It would then be better to convert this to \(m^3\), as follows:
\[27 000 000 \div 1000^3 = 0.027m^3\]Alternatively, you could convert \(300mm\) to \(0.3m\) first and then calculate the surface area using that measurement to give the same result.
Check your understanding of how to calculate the volume of cubes by completing the following activity:
Prisms
The volume of a prism is calculated by multiplying the area of the base by the height of the prism. This section covers one general formula that can be used for all prisms, along with specific formulas for calculating the volume of triangular and rectangular prisms.
Formula for any prism:
\[Volume = Ah\]Where \(A\) is the area of the base and \(h\) is the height of the prism.
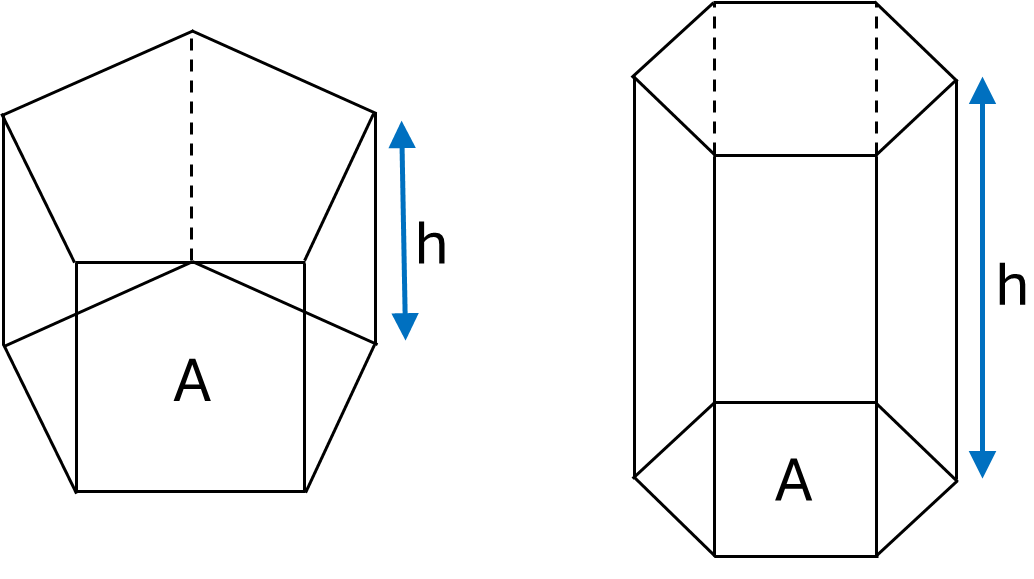
Example: Calculate the volume of a hexagonal prism column with base area \(0.1m^2\) and height \(3m\).
Solution: Using the formula for volume with these measurements gives:
\[Volume = 0.1 \times 3 = 0.3m^3\]\(\)
When the prism is a triangular prism the formula can also be written using dimensions for the base length and height of the triangles, as shown in the following formula.
Formula for a triangular prism:
\[Volume = \frac{1}{2}bhl\]Where \(b\) and \(h\) are the base length and height of the triangles respectively, and \(l\) is the length of the prism.
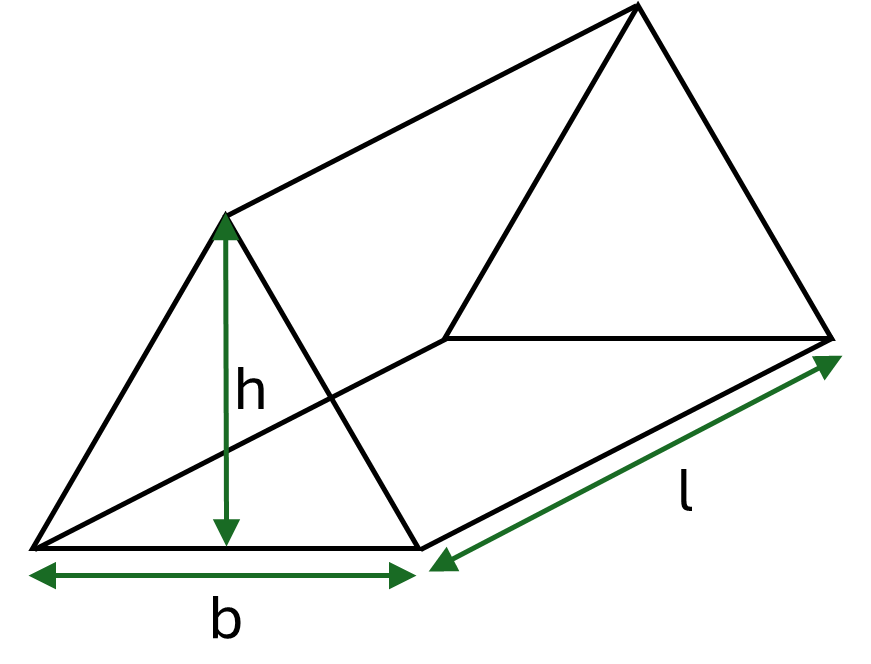
Example: Calculate the volume of a timber triangular prism which has triangles with base \(63.6mm\) and height \(31.8mm\) and length \(2.5m\).
Solution: First we should convert all the units to the same measurement. We will give our final answer in \(m^3\), so we will convert all measurements to \(m\) (although note that you could convert the one measurement that is in \(m\) to \(mm\) here and then convert to \(m^3\) at the end instead if preferred).
\[b = 63.6 \div 1000 = 0.0636m\] \[h = 31.8 \div 1000 = 0.0318m\]We can then use these measurements in the formula to give the following:
\[Volume = \frac{1}{2} \times 0.0636 \times 0.0318 \times 2.5 = 0.0025m^3\]\(\)
Similarly, when the prism is a rectangular prism you may wish to use a formula that uses the dimensions for the length, width and height, as shown in the following formula.
Formula for a rectangular prism:
\[Volume = l \times w \times h\]Where \(l\) is the length of the prism, \(w\) is the width and \(h\) is the height.
Example: Calculate the volume of a timber rectangular prism which is \(1.2m\) long, \(0.03m\) wide and \(0.05m\) high.
Solution: Using the formula with these measurements gives:
\[Volume = 1.2 \times 0.03 \times 0.05 = 0.0018m^3\]Check your understanding of how to calculate the volume of prisms by completing the following activity:
Pyramids
This section covers one general formula that can be used to calculate the volume of all pyramids, along with specific formulas for calculating the volume of regular tetrahedrons and square pyramids.
Formula for any pyramid:
\[Volume = \frac{1}{3}Ah\]Where \(A\) is the area of the base and \(h\) is the height of the pyramid.
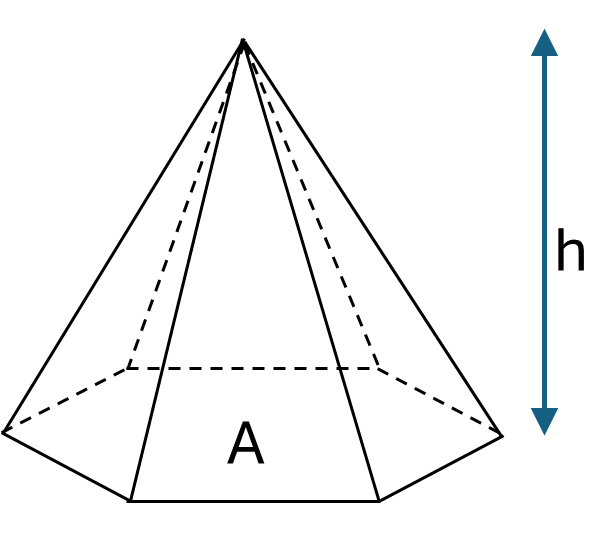
Example: Calculate the volume of a pyramid with base area \(0.35m^2\) and height \(0.4m\).
Solution: Using the formula for volume with these measurements gives:
\[Volume = \frac{1}{3} \times 0.35 \times 0.4 = 0.047m^3\]When the pyramid is a regular tetrahedron you may wish to use a specific formula instead. This formula can be derived using Pythagoras’ theorem, which shows that the area of an equilateral triangle with side length \(b\) is \(\frac{\sqrt{3}}{4}b^2\) and the height of a prism with side length \(b\) is \(\frac{\sqrt{6}}{3}b\)
Formula for a regular tetrahedron:
\[Volume = \frac{b^3}{6\sqrt{2}}\]Where \(b\) is the length of the sides of the equilateral triangles.
Example: Calculate the volume of a regular tetrahedron with side length \(0.6m\)
Solution: Using the formula with this measurement gives:
\[Volume = \frac{0.6^3}{6\sqrt{2}} = 0.025m^3\]\(\)
If you have a square pyramid instead, you can adjust the general formula for volume to incorporate the formula for the area of the square base, as shown in the following formula.
Formula for a square pyramid:
\[Volume \frac{1}{3}s^2h\]Where \(s\) is the length of the sides of the square and \(h\) is the perpendicular height of the pyramid.
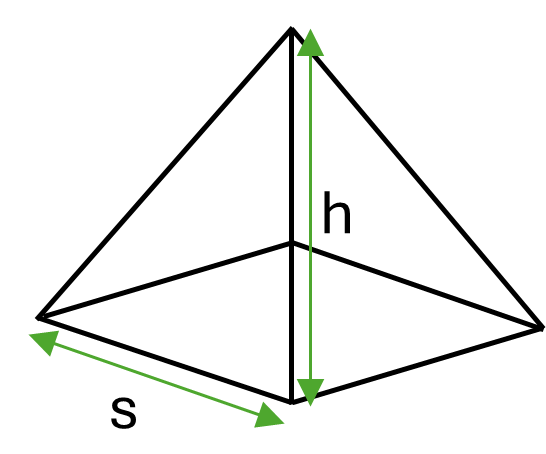
Example: Calculate the volume of a square pyramid with square side length \(30mm\) and perpendicular height \(50mm\).
Solution: Using the formula with these measurements gives:
\[Volume = \frac{1}{3} \times 30^2 \times 50 = 15 000mm^3\]Check your understanding of how to calculate the volume of pyramids by completing the following activity:
Cylinders
The volume of a cylinder is calculated by multiplying the area of the circular base by the height of the cylinder, as shown in the following formula.
Formula for a cylinder:
\[Volume = \pi r^2h\]Where \(r\) is the radius and \(h\) is the height of the cylinder.$$
Example: Calculate the volume of a cylindrical column with radius \(0.15m\) and height \(2.5m\)
Solution: Using the formula for volume with these measurements gives:
\[Volume = \pi \times 0.15^2 \times 2.5 = 0.177m^3\]Check your understanding of how to calculate the volume of cylinders by completing the following activity:
Spheres
The volume of a sphere is equal to four thirds times \(\pi\) times the radius of the sphere cubed, as shown in the following formula.
Formula for a sphere:
\[Volume = \frac{4}{3} \pi r^3\]Where \(r\) is radius of the sphere.
Example: Calculate the volume of a sphere with diameter \(0.7m\)
Solution: First note that the radius of this sphere is \(0.35m\) (i.e. half the diameter). Using the formula for volume with this measurement gives:
\[Volume = \frac{4}{3} \times \pi \times 0.35^3 = 0.180m^3\]Check your understanding of how to calculate the volume of spheres by completing the following activity:
Cones
The volume of a cone is equal to one third times the area of the circular base times the height of the cone, as shown in the following formula.
Formula for a cone:
\[Volume = \frac{1}{3} \pi r^2 h\]Where \(r\) is the radius of the base of the cone and \(h\) is the perpendicular height.
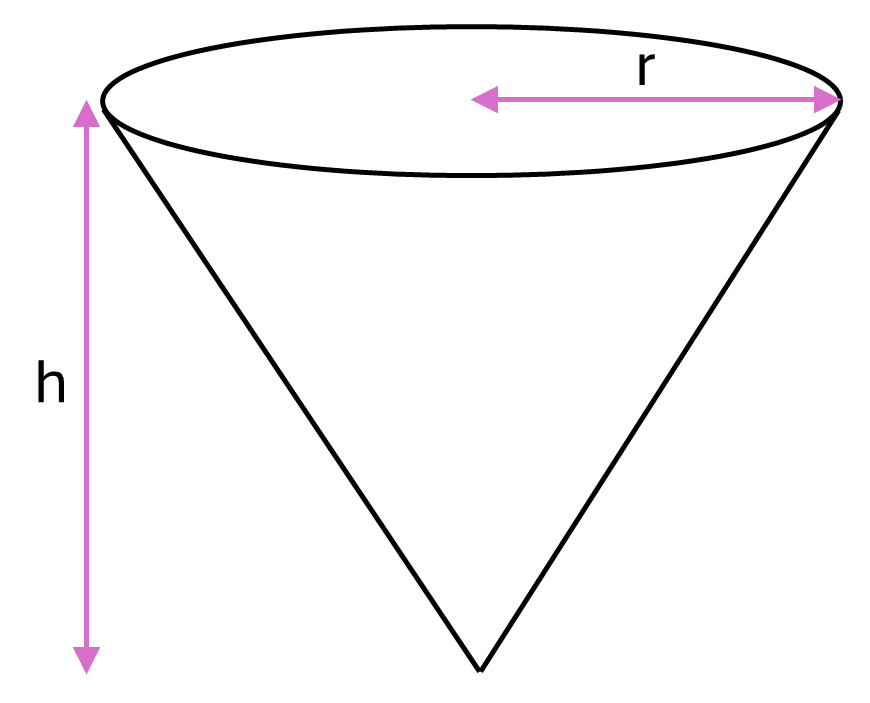
Example: Calculate the volume of a cone with perpendicular height \(0.7m\) and base diameter \(0.3m\)
Solution: First note that the radius of the base of this cone is \(0.15m\) (i.e. half the diameter). Using the formula for volume with this measurement gives:
\[Volume = \frac{1}{3} \times \pi \times 0.15^2 \times 0.7 = 0.016m^3\]If you cut the top off a cone, parallel to the base, the part that is left is called the frustum of the cone. To find the volume of this three-dimensional shape, you can use the following formula.
Formula for the frustum of a cone:
\[Volume = \frac{1}{3} \pi h(r^2 + rR + R^2)\]Where \(r\) is the radius of the top of the frustum of the cone, \(R\) is the radius of the base of the frustum of the cone and \(h\) is the perpendicular height.
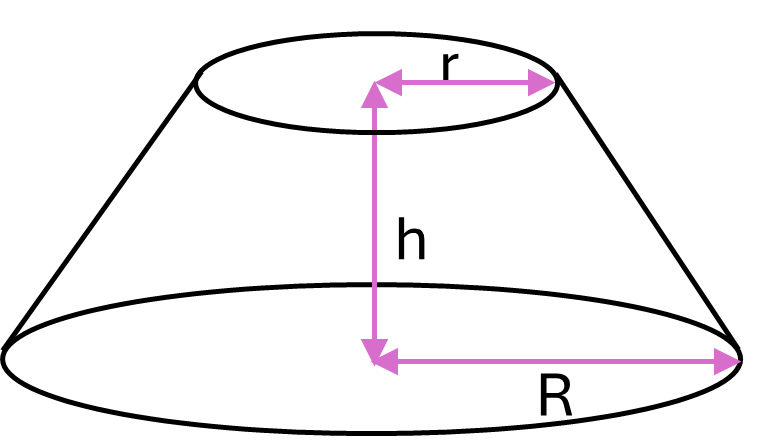
Example: Calculate the volume of a frustum of a cone with perpendicular height \(1.3m\), top radius \(0.2m\) and base radius \(0.45m\).
Solution: Using the formula for volume with these measurement gives:
\[Volume = \frac{1}{3}\times \pi \times 1.3 \times (0.2^2 + 0.2 \times 0.45 + 0.45^2) = 0.453m^3\]Check your understanding of how to calculate the volume of cones by completing the following activity:
Volumes in construction
Sometimes in construction you will need to calculate the volume of a three-dimensional enclosed shape, such as the external walls or concrete footings of a building. In this case the average of the internal and external perimeters (known as the mean girth) should be used for the length measurement. This is then multiplied by the width and depth of the wall or footing to find the volume.
Example: A concrete footing has width \(380mm\), depth \(400mm\) and internal perimeter \(48m\). Calculate the volume of concrete required.
Solution: In order to calculate the volume of concrete required we first need to calculate the mean girth. As detailed in the Perimeter and area page of this module, we can do this as follows (note \(380mm\) has been converted to \(0.38m\)):
\[Mean\textrm{ }girth = 48 + 4 \times 0.38 = 49.52m\]The volume can then be calculated as follows (note \(400mm\) has been converted to \(0.4m\)):
\[Volume = 49.52 \times 0.38 \times 0.4 = 7.527m^3\]Check your understanding of volumes in construction by completing the following activity:
Density
The density of a three-dimensional shape is the amount of matter (or ‘stuff’) it contains per unit volume. Objects with more matter per unit volume (i.e. with a higher density) are said to be more dense than those with less (for example, gold is more dense than wood).
Density can be calculated by dividing the mass of an object by its volume, as shown in the following formula. These measurements are usually in \(kg\) and \(m^3\) respectively, resulting in a density measured in \(kg/m^3\), but other units of measurement can also be used:
\[Density = \frac{Mass}{Volume}\]Note that you can rearrange this formula to calculate the mass or volume from the two other measurements as required. In addition, note that the density of building materials can also be obtained from various references as needed (for example, from Australian Standards and manufacturer data).
Example 1: Determine the density of a rectangular prism concrete block with dimensions \(1.2m\) by \(0.6m\) by \(0.4m\) and with mass \(691kg\)
Solution: Using the formula for the volume of a rectangular prism first gives:
\[Volume = 1.2 \times 0.6 \times 0.4 = 0.288m^3\]Using this value in the formula for density then gives:
\[Density = \frac{691}{0.288} = 2399.31kg/m^3\]Example 2: Determine the mass of a rectangular prism concrete block with dimensions \(0.5m\) by \(0.4m\) by \(0.25m\) given the concrete has a density of \(2200kg/m^3\)
Solution: Using the formula for the volume of a rectangular prism first gives:
\[Volume = 0.5 \times 0.4 \times 0.25 = 0.05m^3\]Rearranging the formula for density and using this value then gives:
\[Mass = Density \times Volume = 2200 \times 0.05 = 110kg\]Example 3: Determine the volume of a concrete block with density \(2300kg/m^3\) and mass \(200kg\)
Solution: Rearranging the formula for density and using these measurements gives:
\[Volume = \frac{Mass}{Density} = \frac{200}{2300} = 0.087kg/m^3\]Check your understanding of density by completing the following activity: