Introduction to calculus
The derivative of a function \(f(x)\) is the rate of change of that function with respect to its input value, \(x\). To find the derivative we use the process of differentiation, and rules for this are covered on this page. First, though, we will delve a bit deeper into the concept of a derivative.
Understanding derivatives
In order to understand derivatives we need to start with the graph of a function, and the slope of that graph.
Consider the graph:
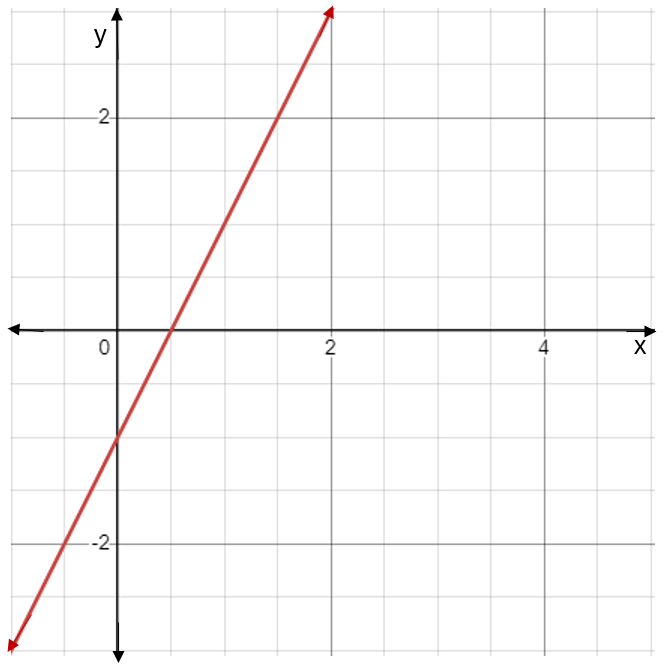
We can find the slope, or gradient, of this graph by choosing two points along the graph and dividing the change in \(y\) by the change in \(x,\) as shown:
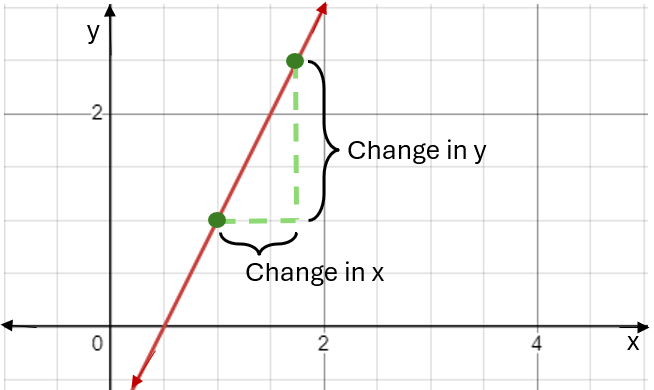
Note that as the function plotted in the graph above is a linear function, the slope is the same at all points on the graph. However, if the function is not linear this is not the case, and instead the slope will be different at different points. In particular, the slope at any given point will be the slope of the tangent to the curve at that point (where the tangent is the straight line that touches the curve at the point). For example, the tangent to the function \(f(x) = x^2 + 1\) at \(x = 0\) is as follows:
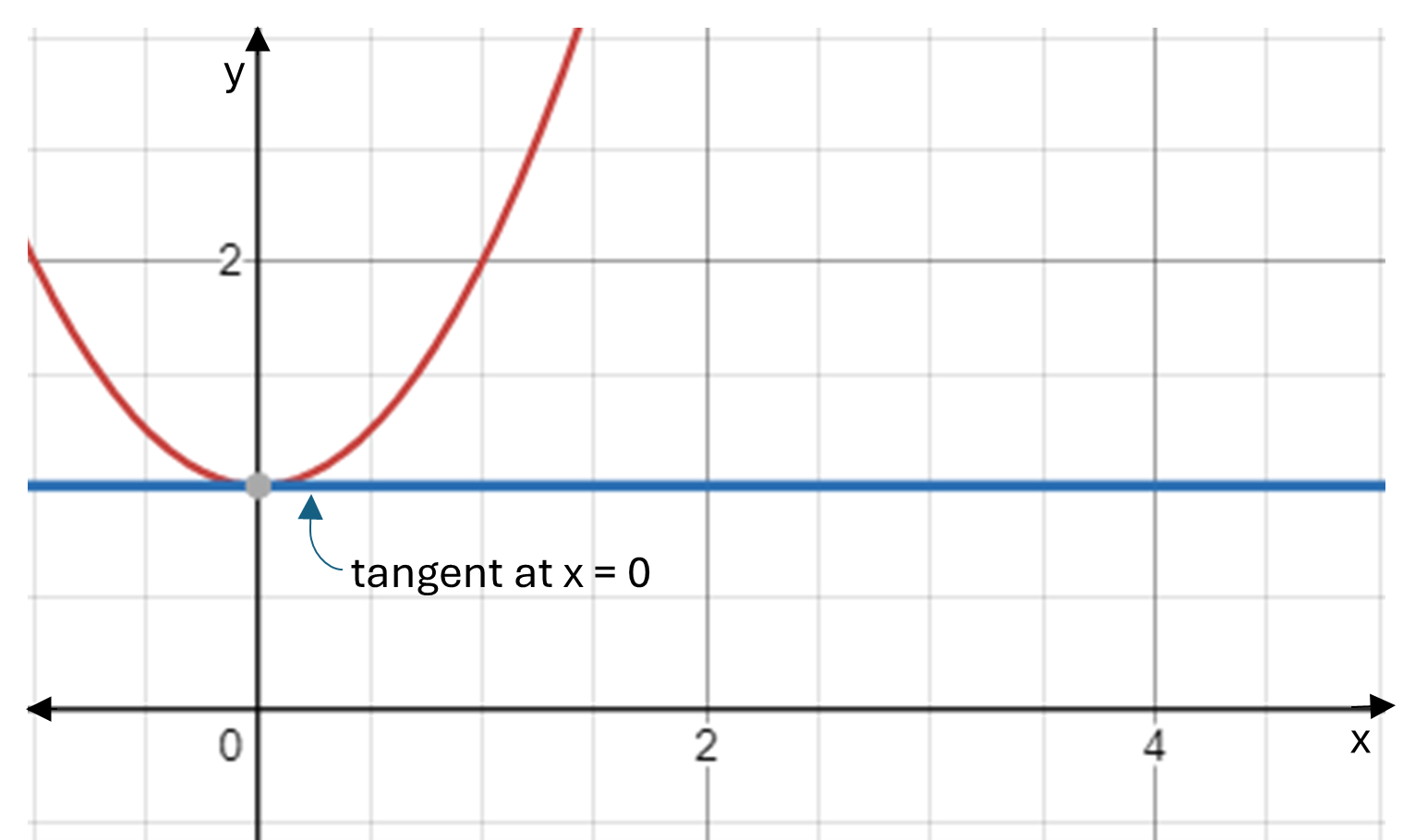
As this tangent is horizontal it has a slope of \(0,\) meaning the slope of \(f(x) = x^2 + 1\) at \(x = 0\) is \(0.\) However, while this is true at this particular point, calculating the slope at other points requires us to calculate the slope of the line between that point and another point as the second point gets closer and closer. In other words, it requires us to find the slope of the line as the difference between the two \(x\) values approaches zero.
In order to do this, we can return to our equation for the slope of a line. Writing change in using the Greek letter delta \(\Delta\) instead, it becomes:
\[Slope\,=\,\frac{\Delta\,y}{\Delta\,x}\]Then as the change in the \(x\) values approaches zero, it can be written as the following limit:
\[\lim_{\Delta x \to 0} \frac{\Delta\,y}{\Delta\,x}\]This is called the derivative of the function. Rather than writing it as above though, we write it as \(\frac{dy}{dx}\)
Alternatively, if we use the function name \(f(x)\) instead we can write the derivative as the following limit, where \((x, f(x))\) is the point of interest and \(h\) is the difference between this and the second point, \((x+h, f(x+h)):\)
\[\lim_{h \to 0} \frac{f(x + h) - f(x)}{h}\]Example:
Find the derivative of \(f(x) = x^2 + 1\)
Solution:
Substituting this function into the limit above gives:
\[\begin{aligned} \lim_{h \to 0} \frac{((x+h)^2 + 1) - (x^2 + 1)}{h} &= \lim_{h \to 0} \frac{x^2 + 2xh + h^2 + 1 - x^2 - 1}{h}\\\ &= \lim_{h \to 0} \frac{2xh + h^2}{h}\\\ &= \lim_{h \to 0} 2x + h\\\ &= 2x\\\ \end{aligned}\]So the derivative of this function is \(2x\)
In this case, the derivative of the function is called the prime of the function and is written as \(f'(x)\). This is read as f-prime of \(x\) and means the derivative of \(f(x)\) with respect to \(x\).
Therefore, if \(y\,=\,f(x)\), the derivative of that function will be written as:
\[\frac{dy}{dx}\;\]or
\[f'(x)\](It may also be written as \(\frac{d}{dx}\,y\) or \(\frac{d}{dx}\,f(x),\) but this notation won’t be used here.)
Note that the derivatives discussed so far are referred to as first derivatives, as we are only differentiating once. While these are the only kinds of derivatives covered on this page, it is important to be aware that you can differentiate again to give the second derivative \(\frac{d^2y}{dx^2},\) and again to give the third derivative \(\frac{d^3y}{dx^3},\) and so on.
Differentiation rules
Rather than calculating the limit each time as above, there are a set of general rules to follow in order to find the derivative of any given function. You may need to use any number of these rules, depending on the elements within the function, in order to find the derivative.
Constant rule
The derivative of a constant number, \(c\), is always zero.
If
\[f(x)\,=\,c\]then
\[f'(x)\,=\,0\]Example:
Find the derivative of \(f(x)\,=\,3\)
Solution:
Using the constant rule, \(f'(x)\,=\,0\)
Line rule
When \(x\) has a coefficient, the derivative will just be the coefficient.
If
\[f(x)\,=\,nx\]then
\[f'(x)\,=\,n\]Example:
Find the derivative of:
\[f(x)\,=\,7x\]Solution:
\[f'(x)\,=\,7\]Power rule
When \(x\) has an indice, multiply \(x\) by that indice, and then reduce the indice by one.
If
\[f(x)\,=\,x^n\]then
\[f'(x)\,=\,n\,x^{n-1}\]Example 1:
What is \(f'(x)\) given \(f(x)\,=\,x^4\)
Solution:
\[f'(x)\,=\,4x^3\]Example 2:
What is the derivative of \(y\,=\,3\,x^2\)
Solution:
\(\begin{aligned} \frac{dy}{dx} &= 2 \times 3x^{2-1} \\\ &= 6x \\\ \end{aligned}\)
Trigonometric function rules
We can also find the derivatives of the trigonometric functions \(sin\), \(cos\), and \(tan\). It’s important to note that when working with the derivatives of trigonometric functions, \(x\) will be in radians.
The derivative of \(sin\) is \(cos\). So if
\[f(x)\,=\,sin\,x\]then
\[f'(x)\,=\,cos\,x\]The derivative of \(cos\) is negative \(sin\). So if
\[f(x)\,=\,cos\,x\]then
\[f'(x)\,=\,-\,sin\,x\]And the derivative of \(tan\) is \(sec^2\), where \(sec\) is another trigonometric function. So if
\[f(x)\,=\,tan\,x\]then
\[f'(x)\,=\,sec^2\,x\]Example:
If \(f(x)\,=\,2sin\,x\;+\;cos\,x\), find \(f'(x)\)
Solution:
\[f'(x)\,=\,2cos\,x\;-\;sin\,x\]Taking it further, when \(x\) has a coefficient in a trigonometric function, the derivative is multiplied by this coefficient.
Example:
If \(f(x)\,=\,2tan\,2x\), find \(f'(x)\)
Solution:
Since the \(x\) in the trigonometric function has a coefficient of \(2\), our solution will be:
\[\begin{aligned} f'(x) &= 2 \times 2\,sec^2\,2x \\\ &= 4\,sec^2\,2x \\\ \end{aligned}\]Euler’s number
To find the derivative of a power function of Euler’s number, \(e\), simply multiply the function by the derivative of the power.
If
\[y = e^{f(x)}\]then
\[\frac{dy}{dx} = f'(x)\,e^{f(x)}\]Example:
Find the derivative of \(f(x) = e^x\)
Solution:
\[\begin{aligned} f'(x) &= 1 \times e^x \\\ &= e^x \\\ \end{aligned}\]Example 2:
Find the derivative of \(f(x) = e^{3x^5 + 1}\)
Solution:
\[f'(x) = 15x^4\,e^{3x^5 + 1}\]Logarithms
You may also have to find the derivatives of functions containing logarithms.
If
\[f(x) = log_a\,x\]then
\[f'(x) = \frac{1}{x\,ln\,a}\]Example 1:
Find the derivative of \(f(x) = log_2\,x\)
Solution:
\(\begin{aligned}
f'(x) &= \frac{1}{x\,ln\,a} \\\
&= \frac{1}{x\,ln\,2} \\\
\end{aligned}\)
Example 2:
Find the derivative of \(f(x) = log_{10}\,{5x}\)
Solution:
Using the logarithm laws we have:
\[f(x) = log_{10}\,5 + log_{10}\,x\]Since \(log_{10}\,5\) is a constant, it’s derivative will be \(0\). Therefore \(f(x) = log_{10}\,x\) is the only part that needs to be differentiated:
\[f'(x) = \frac{1}{x\,ln\,{10}}\]If your logarithm is the natural logarithm \(ln,\) the derivative is simplified.
If
\[f(x) = ln\,x\]then
\[f'(x) = \frac{1}{x}\]Example 1:
Find the derivative of \(f(x) = ln\,{3x}\)
Solution:
Using log laws, we know that:
\[f(x) = ln\,3 + ln\,x\]Since \(ln\,3\) is a constant, we have:
\[f'(x) = \frac 1x\]Example 2:
Find the derivative of \(f(x) = ln(x^2)\)
Solution:
Using log laws, we know that:
\[f(x) = 2\,ln\,x\]Therefore, we have:
\[\begin{aligned} f'(x) &= 2 \times \frac 1x \\\ &= \frac 2x \\\ \end{aligned}\]Note: To differentiate logarithms of functions, you will need to use the chain rule.
Test your knowledge of the above differentiation rules by having a go at finding the derivatives of the functions below:
Using log laws, we know that
\[f(x) = 3 log_4 x\]So the derivative will be
\[\begin{aligned} f'(x) &= 3(\frac{1}{xln4}) \\\ &= \frac{3}{xln4} \\\ \end{aligned}\]Two functions
You may have to use differentiation to find the derivatives of two related functions, for example \(f(x)\) and \(g(x).\) How these functions are related will determine which rule you use to find the derivative.
Sum and difference
When two functions are added together or subtracted from each other, we find the derivative of each function and keep the relevant operation.
If
\[y\,=\,f(x)\,\pm\,g(x)\]then
\[\frac{dy}{dx}\,=\,f'(x)\,\pm\,g'(x)\]Example:
Find the derivative of \(y\) given that \(y\,=\,f(x)\,+\,g(x),\) \(f(x)\,=\,4x\,+2\) and \(g(x)\,=\,3x^2\)
Solution:
\(f'(x)\,=\,4\) and \(g'(x)\,=\,6x,\) therefore:
\[\frac{dy}{dx}\,=\,4\,+\,6x\]Test your knowledge of the sum and difference rule by using it to find the derivatives of the functions below:
Which is then simplified to be:
\[f'(x) = -12x^2 + 10x + 5\]Product rule
The product rule is used when two functions are being multiplied together.
If we have
\[y\,=\,f(x)\,\times\,g(x)\]then the derivative will be
\[\frac{dy}{dx}\,=\,g(x)\,\times\,f'(x)\;+\;f(x)\,\times\,g'(x)\]Example:
Given \(y\,=\,(3x\,+\,4) \times (2x^3\,+\,x\,-\,7)\), use the product rule to find \(\frac{dy}{dx}\)
Solution:
Let \(f(x)=3x\,+\,4\) and \(g(x)=2x^3\,+\,x\,-\,7\)
We can now use the product rule to find \(\frac{dy}{dx}\)
\[\begin{aligned} \frac{dy}{dx} &= g(x)\,\times\,f'(x)\;+\;f(x)\,\times\,g'(x) \\\ &= (2x^3\,+\,x\,-\,7) \times (3)\;+\;(3x\,+\,4) \times (6x\,+\,1) \\\ \end{aligned}\]We then simplify the expression:
\[\begin{aligned} \frac{dy}{dx} &= (2x^3\,+\,x\,-\,7) \times (3)\;+\;(3x\,+\,4) \times (6x\,+\,1) \\\ &= 6x^3\,+\,3x\,-\,21\,+\,18x^2\,+\,3x\,+\,24x\,+\,4 \\\ &= 6x^3\,+\,3x\,-\,21\,+\,18x^2\,+\,27x\,+\,4 \\\ &= 6x^3\,+\,18x^2\,+\,30x\,-\,17 \\\ \end{aligned}\]Test your knowledge of the product rule by using it to find the derivatives of the functions below:
Which can then be expanded and simplified to:
\[f'(x) = 40x^4 + 42x^2 - 15\]Which can then be expanded and simplified into:
\[f'(x) = 12x^3 - 6x^2 + 6\]Quotient rule
The quotient rule is used when one function is being divided by another.
If we have
\[y\,=\,\frac{f(x)}{g(x)}\]then the derivative will be
\[\frac{dy}{dx}\,=\,\frac{g(x)\,\times\,f'(x)\;-\;f(x)\,\times\,g'(x)}{(g(x))^2}\]Example:
Find \(\frac{dy}{dx}\) given \(y=\frac{3x+5}{2x-2}\)
Solution:
Let \(f(x)=3x+5\) and \(g(x)=2x-2\)
We can now find \(\frac{dy}{dx}\) using the quotient rule.
\[\begin{aligned} \frac{dy}{dx} &= \frac{g(x)\,\times\,f'(x)\;-\;f(x)\,\times\,g'(x)}{(g(x))^2} \\\ &= \frac{(2x-2) \times (3)\;-\;(3x+5) \times (2)}{(2x-2)^2} \\\ \end{aligned}\]We then simplify the expression:
\[\begin{aligned} \frac{dy}{dx} &= \frac{(2x-2) \times (3)\;-\;(3x+5) \times (2)}{(2x-2)^2} \\\ &= \frac{(6x-6)\,-\,(6x+10)}{(2x-2)^2} \\\ &= -\,\frac{16}{(2x-2)^2} \\\ \end{aligned}\]Test your knowledge of the quotient rule by using it to find the derivatives of the functions below:
Which we can then expand and simplify into:
\[\frac{dy}{dx} = \frac{4x^2 + 10x - 8}{(x^2 + 2)^2}\]Which can then be simplified into:
\[\frac{dy}{dx} = \frac{10x\,cos\,3x + 15x^2sin\,3x + 9sin\,3x}{(cos\,3x)^2}\]Chain rule
The chain rule applies when one function relies on the answer from another function, or when one function contains another function.
For example, if we have a function \(y\) that contains the variable \(u\), and we have a function \(u\) that contains the variable \(x\), in order to find the derivative \(\frac{dy}{dx}\) we would first need to find \(\frac{dy}{du}\) and then \(\frac{du}{dx}\). The chain rule says we can then multiply these together to get \(\frac{dy}{dx}\).
If we want to find \(\frac{dy}{dx}\) and we know \(\frac{dy}{du}\) and \(\frac{du}{dx}\) then
\[\frac{dy}{dx}\,=\,\frac{dy}{du}\,\times\,\frac{du}{dx}\]Example 1:
Find \(\frac{dy}{dx}\) given \(y\,=\,10u\) and \(u\,=\,-4x^2\,+\,2x\)
Solution:
The first thing we have to do is find \(\frac{dy}{du}\):
Next, we need to find \(\frac{du}{dx}\):
\[\begin{aligned} \frac{du}{dx} &= 2 \times (-4)x^{2-1}\,+\,2 \\\ &= -8x\,+\,2 \\\ \end{aligned}\]Now, using the chain rule, we can find \(\frac{dy}{dx}\):
\[\begin{aligned} \frac{dy}{dx} &= \frac{dy}{du}\,\times\,\frac{du}{dx} \\\ &= 10 \times (-8x\,+\,2) \\\ &= -80\,x\,+\,20 \\\ \end{aligned}\]Example 2:
We can use the chain rule to differentiate the logs of functions. As an example, find the derivative of \(y = ln(2x^2 + 3)\)
Solution:
Let \(u = 2x^2 + 3,\) so \(y = ln\,u\) and we have \(\frac{du}{dx} = 4x\) and \(\frac{dy}{du} = \frac{1}{u}.\) Our integral can then be evaluated as follows:
\[\begin{aligned} \frac{dy}{dx} &= \frac{dy}{du} \times \frac{du}{dx} \\\ &= \frac{1}{u} \times 4x \\\ &= \frac{4x}{u} \\\ &= \frac{4x}{2x^2 + 3} \\\ \end{aligned}\]Test your knowledge of the chain rule by using it to find the derivatives of the functions below:
Let \(u = 2x^2 + 1,\) so \(y = cos\,u\) and we have \(\frac{du}{dx} = 4x\) and \(\frac{dy}{du} = -sin\,u.\) Our derivative can then be evaluated as follows:
\[\begin{aligned} \frac{dy}{dx} &= \frac{dy}{du} \times \frac{du}{dx} \\\ &= -sin\,u \times 4x \\\ &= -4x\,sin\,u \\\ &= -4x\,sin(2x^2 + 1) \\\ \end{aligned}\]Let \(u=3x^2 + 2,\) so \(y = u^4\) and we have\(\frac{du}{dx} = 6x\) and \(\frac{dy}{du} = 4u^3.\) Our derivative can then be evaluated as follows:
\[\begin{aligned} \frac{dy}{dx} &= \frac{dy}{du} \times \frac{du}{dx} \\\ &= 4u^3 \times 6x \\\ &= 4(3x^2 + 2)^3 \times 6x \\\ &= 24x(3x^2 + 2)^3 \\\ \end{aligned}\]Let \(u = 3x^2 + 1,\) so \(y = log_5\,u\) and we have \(\frac{du}{dx} = 6x\) and \(\frac{dy}{du} = \frac{1}{u\,ln\,5}.\) Our derivative can then be evaluated as follows:
\[\begin{aligned} \frac{dy}{dx} &= \frac{dy}{du} \times \frac{du}{dx} \\\ &= \frac{1}{u\,ln\,5} \times 6x \\\ &= \frac{6x}{u\,ln\,5} \\\ &= \frac{6x}{(3x^2 + 1)\,ln\,5} \\\ \end{aligned}\]\(\frac{du}{dx} = cos\,x\) and \(\frac{dy}{du} = 10u + 2,\) so our derivative can be evaluated as follows:
\[\begin{aligned} \frac{dy}{dx} &= \frac{dy}{du} \times \frac{du}{dx} \\\ &= (10u + 2) \times cos\,x \\\ &= (10\,sin\,x + 2)(cos\,x) \\\ \end{aligned}\]