Introduction to calculus
Limits are an important concept in calculus, as they are used to define continuity, derivatives and integrals. This page introduces limits and continuity, while subsequent pages explore derivatives and integration.
Limits
Suppose we have a function \(f(x)\) and we investigate the value this function approaches as the input value \(x\) approaches a particular value, which we will call \(a.\) In this case we say we are finding the limit of \(f(x)\) as \(x\) approaches \(a,\) and we use the following notation to represent this:
\[\lim_{x \to a} f(x)\]Furthermore, sometimes we need to indicate whether we are approaching \(a\) from the left or the right, as the limit does not always give the same value. In this case we use the notation \(\lim_{x \to a^-} f(x)\) to indicate a left hand limit, and \(\lim_{x \to a^+} f(x)\) to indicate a right hand limit.
Note that in order for \(\lim_{x \to a} f(x)\) to exist, \(\lim_{x \to a^-} f(x)\) and \(\lim_{x \to a^+} f(x)\) need to be the same.
We can calculate the left hand and right hand limits of a function, and therefore determine if the limit of that function exists as \(x\) approaches a given value, using tables of values.
Example 1:
Use tables of values to investigate \(\lim_{x \to 3} (x^2 + 4x + 5)\)
Solution:
Limit as \(x\) approaches \(3\) from the left:
| \(x\) | \(x^2 + 4x + 5\) |
|---|---|
| 2.9 | 25.01 |
| 2.99 | 25.9001 |
| 2.999 | 25.990001 |
| 2.9999 | 25.99900001 |
Limit as \(x\) approaches \(3\) from the right:
| \(x\) | \(x^2 + 4x + 5\) |
|---|---|
| 3.1 | 27.01 |
| 3.01 | 26.1001 |
| 3.001 | 26.010001 |
| 3.0001 | 26.00100001 |
These tables indicate that:
\(\lim_{x \to 3^-} (x^2 + 4x + 5) = \lim_{x \to 3^+} (x^2 + 4x + 5) = 26\)
Therefore:
\(\lim_{x \to 3} (x^2 + 4x + 5) = 26\)
The fact that \(\lim_{x \to 3} (x^2 + 4x + 5) = 26\) should not be surprising, as this is the value of \(x^2 + 4x + 5\) when \(x = 3\). In other words, \(\lim_{x \to 3} (x^2 + 4x + 5) = f(3)\)
In fact, the following is true for any function that is continuous at \(x = a\):
\(\lim_{x \to a} f(x) = f(a)\)
More information on continuity, and the conditions required for a function to be continuous at \(x = a,\) are covered in the following section.
Example 2:
Use tables of values to investigate \(\lim_{x \to 2} (\frac{1}{x-2})\)
Solution:
Limit as \(x\) approaches \(2\) from the left:
| \(x\) | \(x^2 + 4x + 5\) |
|---|---|
| 1.9 | -10 |
| 1.99 | -100 |
| 1.999 | -1000 |
| 1.9999 | -10000 |
| 1.99999 | -100000 |
Limit as \(x\) approaches \(2\) from the right:
| \(x\) | \(x^2 + 4x + 5\) |
|---|---|
| 2.1 | 10 |
| 2.01 | 100 |
| 2.001 | 1000 |
| 2.0001 | 10000 |
| 2.00001 | 100000 |
These tables indicate that:
\(\lim_{x \to 2^-} (\frac{1}{x-2}) = -\infty\)
\(\lim_{x \to 2^+} (\frac{1}{x-2}) = \infty\)
Therefore:
\(\lim_{x \to 2} (\frac{1}{x-2})\) does not exist
Note that while technically speaking a limit can not equal positive or negative infinity, and therefore if it tends towards one of these the limit does not exist, by stating that the limit tends towards positive or negative infinity (as above) we provide more information about the behaviour of the function close to the specified point.
Note also that the fact this limit does not exist means this function is not continuous. Again, more information is provided on continuity in the following section.
For now though, test your understanding of limits by working through the questions below:
Using tables of values, or by substituting \(x = 3\) into the function (since it is continuous at this point), we can determine that \(\lim_{x \to 3} (x^2 + 4) = 13\)
Using tables of values, we can determine that \(\lim_{x \to 1} (\frac{x^2-3x+2}{x-1}) = -1\)
Using tables of values, we can determine that this limit does not exist. If we want to provide more information about the limit, however, we could state that:
- \(\lim_{y \to -5^-} (\frac{y^2+4}{y+5}) = -\infty\)
- \(\lim_{y \to -5^+} (\frac{y^2+4}{y+5}) = \infty\)
Using tables of values, or by substituting \(x = 2\) into \(f(x) = 5 - x^2\), we can determine that:
\(\lim_{x \to 2^-} f(x) =1\)
Similarly, using tables of values or by substituting \(x = 2\) into \(f(x) = x - 1\), we can determine that:
\(\lim_{x \to 2^+} f(x) =1\)
Therefore, \(\lim_{x \to 2} f(x) =1\)
Continuity
If the graph of a function does not have any breaks or jumps in it (in other words, if you could draw the function without lifting your pencil from the paper) then that function is continuous everywhere. Note that even if a function is not continuous everywhere, often it is continuous except at a single value of \(x.\)
For example:
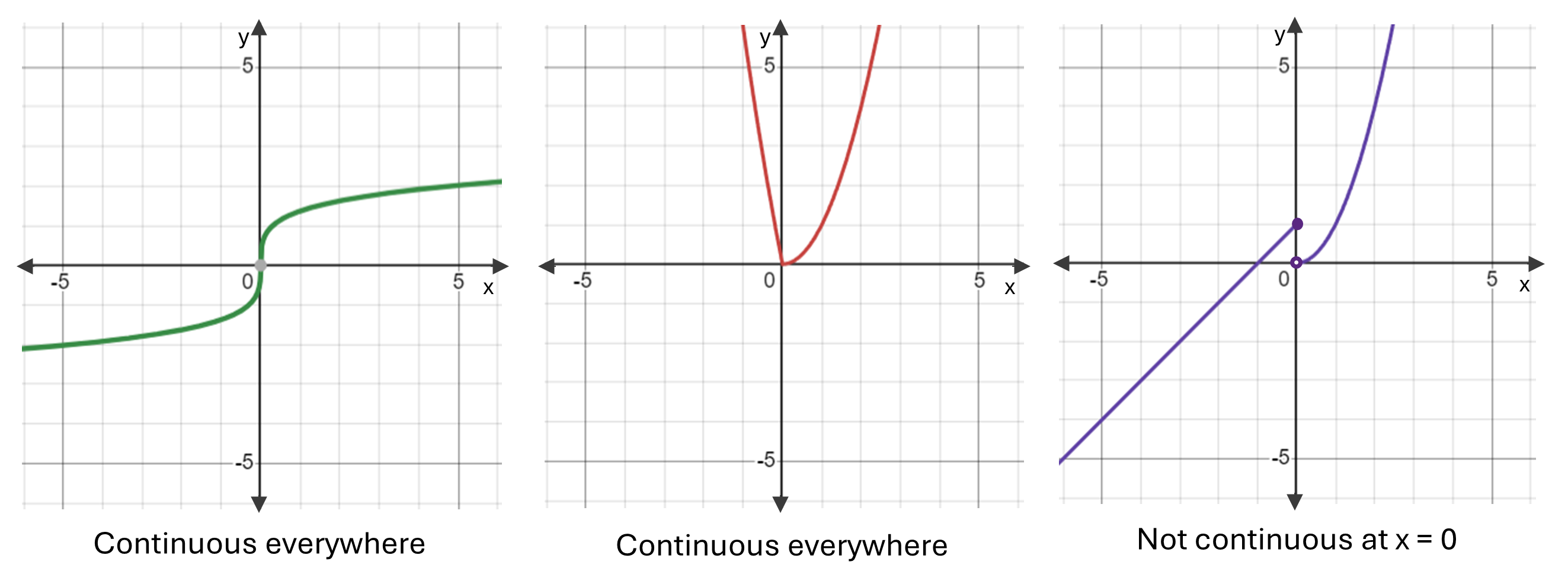
While the above is a good way of thinking about continuity, there is also a formal mathematical definition for it. This says that for a function \(f(x)\) to be continuous at \(x = a\) all of the following must be true:
- The function must exist at \(x = a\)
- \(\lim_{x \to a}f(x)\) must exist, i.e. \(\lim_{x \to a^-}f(x) = \lim_{x \to a^+}f(x)\)
- \(\lim_{x \to a}f(x)\) must equal \(f(a)\)
Example:
Is the function \(f(x) = \frac{x+4}{x^2 + 3x - 40}\) continuous? If not, for which value or values is it discontinuous?
Solution:
Noting that dividing by \(0\) is undefined, we can factorise the denominator of this function to find the values of \(x\) such that it is equal to \(0.\) Factorising gives the following:
\(f(x) = \frac{x+4}{(x+8)(x-5)}\)
Finding the values of \(x\) such that \((x+8)(x-5) = 0\) gives \(x = -8\) and \(x = 5,\) which means the function is discontinuous at these values.
All polynomials are continuous everywhere. Furthermore, if two functions \(f(x)\) and \(g(x)\) are both continuous at \(x = a\) then:
- \(k f(x)\) is continuous at \(x = a\) (where \(k\) is any real number)
- \(f(x) + g(x)\) is continuous at \(x = a\)
- \(f(x) - g(x)\) is continuous at \(x = a\)
- \(f(x) \times g(x)\) is continuous at \(x = a\)
- \(f(x) \div g(x)\) is continuous at \(x = a\), as long as \(g(a) \neq 0\)
Test your understanding of continuity by working through the questions below:
Yes, this function is continuous everywhere as it is a polynomial.
The denominator of this function is equal to \(0\) when \(x = 3,\) hence the function is discontinuous when \(x = 3\)
Factorising the denominator of this function gives:
\(f(x) = \frac{x - 2}{(x+8)(x+2)}\)
Since you can’t divide by \(0\) we need to find the values for \(x\) such that \((x+8)(x+2) = 0,\) which gives \(x = -8\) and \(x = -2\)
This means the function is discontinuous at these values.
\(h(x) = f(x) + g(x),\) and since \(f(x)\) and \(g(x)\) are both continuous at \(x = 1\) it follows that \(h(x)\) must also be continuous at \(x = 1\)