Introduction to algebra

This page introduces the concept of a function, and details some common types including linear, quadratic, exponential and logarithmic functions.

What is a function?

A function in mathematics is a relationship between input values and output values, whereby each input value has exactly one output value. This relationship can be visualised as follows:

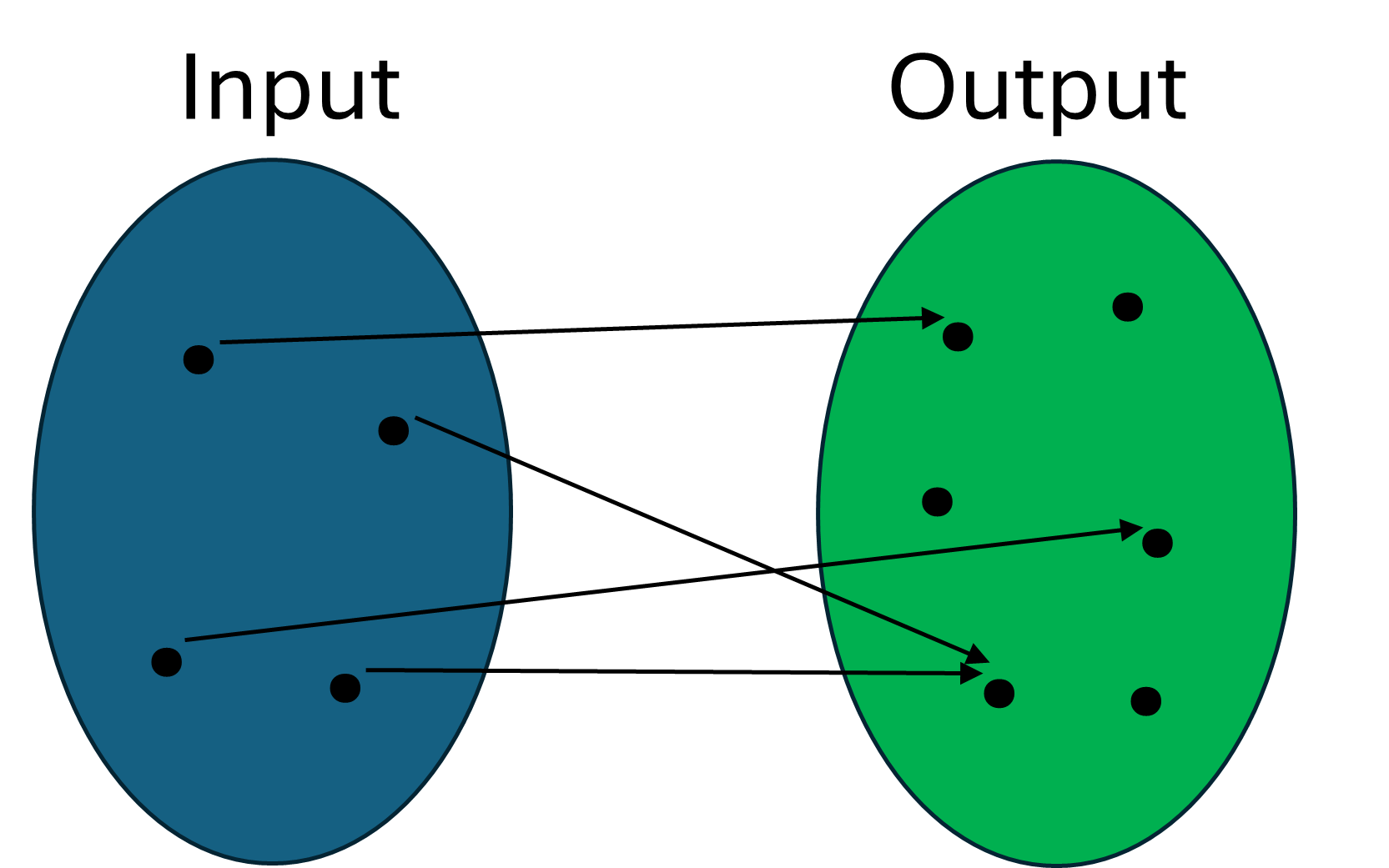
Two ovals, one labelled 'input' and one labelled 'output'. Both ovals contain small black circles representing values. The four values in the 'input' oval map to values in the 'output' oval, with two of them mapping to the same output value.

From this image, note that the set of input values is called the domain of the function, the set of all possible output values is called the codomain, and the set of output values that are actually mapped to by the input values is called the range.

Also note that while it is fine for multiple input values to be mapped to the same output value, as shown, one input value can not map to multiple output values as this violates the definition of a function.

As an example of a function, consider the linear relationship:

\[y = 2x + 3\]

This function takes a number \(x\) and transforms it by multiplying it by \(2\) and adding \(3,\) in order to produce an output value called \(y.\) Some examples of these input and output values are as follows:

Input value (x) Output value (y)
-1 1
0 3
1 5
2 7

Note that the function \(y = 2x + 3\) works for all real numbers, but this is not always the case. Sometimes in order for a relationship to be a function, the domain and/or codomain needs to be restricted. For example, the relationship \(y = \sqrt{x}\) does not provide any (real) output values for negative input values, and it provides two output values for each positive input value (for example, the square root of \(9\) is both \(-3\) and \(3).\) Therefore, it is only a function if both the domain and codomain are limited to non-negative real numbers.

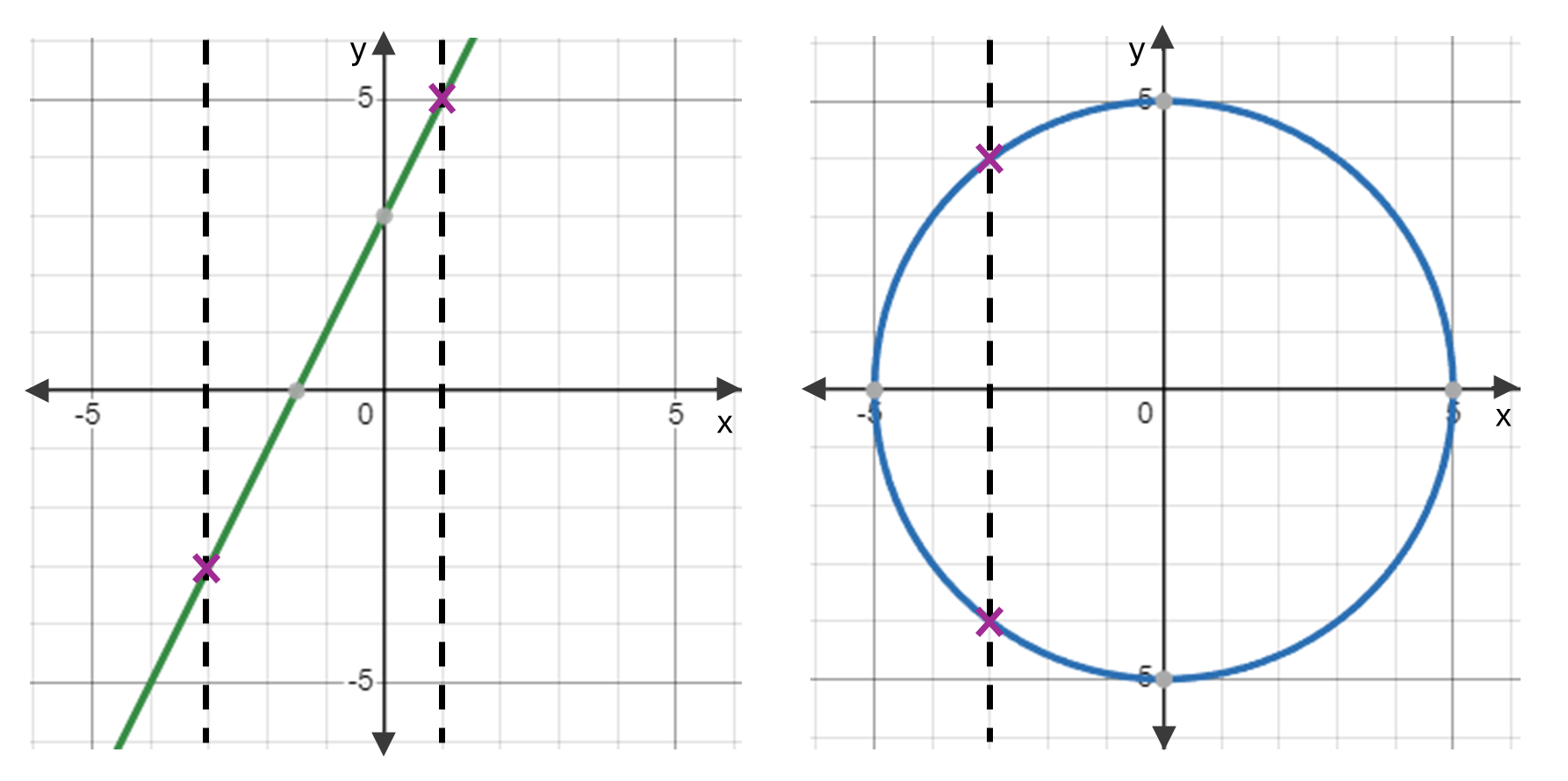
Note also that if you have a graph of a relationship, you can determine whether it is a function by performing the vertical line test. This test says that the relationship is a function if and only if each vertical line intersects the graph no more than once. For example, the relationship on the left (which is \(y = 2x + 3\)) is a function as it is not possible to draw a vertical line that intersects the graph more than once at any point. However, the relationship on the right is not a function as there is at least one point (in fact there are many) where a vertical line intersects the graph twice.

Plots of two relationships. The first relationship is a function as a vertical line at any point only intersects the graph once. The second relationship is not a function as a vertical line intersects the graph twice at some points.

Check your understanding of functions by completing the following activity:

Function names

A function can just be stated in terms of \(x\) and \(y\) (or other variable names as relevant), as per the function \(y = 2x + 3\) stated previously. However, generally functions are given ‘names’, of which \(f\) is the most common. For example, the linear function \(y = 2x + 3\) could be written as:

\[f(x) = 2x + 3\]

where:

  • \(f\) is the name of the function, and we say \(f\) of \(x\) is equal to \(2x + 3\)
  • \(x\) is the input value of the function.

If we had an input value of \(x = 2\) for this function, for example, then we could write the following (note this matches with the \(y\) value as shown in the table above):

\[f(2) = 7\]

Check your understanding of function names by completing the following activity:

\(f(z) = z^2 + 7\)

\(f(10) = 25\)

Types of functions

There are many different types of functions, but here we will consider four types based on what has been covered in this module. These are as follows:

  • Linear functions: Linear equations in two variables are functions, and in particular they are linear functions. For example, \(f(x) = 2x + 3\) is a linear function.

  • Quadratic functions: Quadratic functions are of the form \(f(x) = ax^2 + bx + c, \) where \(a \neq 0.\) For example, \(f(x) = 2x^2 + 3x -2\) is a quadratic function.

  • Exponential functions: Exponential functions are of the form \(f(x) = a^x,\) where \(a > 0.\) For example, \(f(x) = 3^x\) is an exponential function.

  • Logarithmic functions: Logarithmic functions are of the form \(f(x) = \log_a{x},\) where \(a >0\) and \(a \neq 1.\) For example, \(f(x) = log_{10}{x}\) is a logarithmic function.

Check your understanding of different types of functions by completing the following activity:

This is an exponential function.

This is a quadratic function.