Introduction to algebra
In order to solve algebraic equations to find unknown values, which is a central focus of algebra, you first need to have an understanding of the key algebraic terms and techniques detailed in this page.
In brief, these are as follows:
- Definitions of some important algebraic terms
- How to simplify algebraic expressions
- How to expand brackets in algebraic expressions
- How to factorise algebraic expressions
Definitions of important terms
When a problem is written in the language of algebra we call it either an algebraic expression (when there is no equals sign), or an algebraic equation (when there is an equals sign). Both algebraic expressions and algebraic equations involve the use of constants and variables:
Constants are numbers with a fixed or constant value (for example \(1, 5, 2108, 37.5, -103,\) etc.).
Variables are small letters of the alphabet, or indeed any symbols, used to represent some unknown number in an expression or equation (for example \(x, y, a, \theta,\) etc.). The value of this number can vary (as the word variable suggests) according to the context.
In the algebraic expression \(a + 5,\) for example, \(5\) is a constant while \(a\) is a variable. This means that different numbers can be substituted for \(a\) and the value of the expression will change accordingly. For example, if \(a = 1\) then \(a + 5\) becomes \(1 + 5,\) which we know to be equal to \(6\).
Another thing to be aware of is that every ‘part’ of an algebraic expression or equation separated from other ‘parts’ by addition, subtraction or division (be it a constant, a variable or variables, or a combination of constants and variables), is referred to as a term. For example, the following algebraic expression contains \(5\) different terms, each separated by addition (note that we simply write \(x\) and \(y\) rather than \(1x\) and \(1y\), although they represent the same thing):
\[2x + y + 3y + 5x + x\]Furthermore, as this expression contains more than one variable, we say that it consists of like and unlike terms:
Like terms are terms which have the same variable. For example \(2x,\) \(5x\) and \(x\) are all like terms in the above expression. Similarly, \(y\) and \(3y\) are like terms.
Note that \(x\) and \(x^2\) are not like terms as one of the terms has an \(x\) only while the other has an \(x\) raised to the power of \(2.\) Similarly, \(x\) and \(xy\) are not like terms as one has an \(x\) only while the other has an \(x\) and a \(y.\)
Unlike terms are terms which have different variables. For example \(2x\) and \(y\) are unlike terms in the above expression. Similarly, as described above, \(x\) and \(x^2\) are unlike terms, and so too are \(x\) and \(xy\).
It is important to understand that only like terms can be added and subtracted. You wouldn’t say that \(2\) apples plus \(5\) oranges equals \(7\) apples (or \(7\) oranges), and similarly you can’t add \(2x\) and \(5y\) together.
Finally, when we combine terms together in a certain way they create polynomials:
A polynomial is an expression that consists of constants and/or variables raised to positive exponents, combined using addition, subtraction, and/or multiplication. For example, \(x^2 + 2x - 3\) is a polynomial, and so is \(20\), but \(x^{-2} + 3\) is not.
Simplifying algebraic expressions
As with most things, it is best to write an algebraic expression or equation in the simplest way possible - no need to make it any more confusing than necessary! There are a couple of key things you can do to simplify algebraic expressions and equations, and these are detailed in this section.
Note that the examples refer to algebraic expressions as it is easiest to learn the techniques with these first, but do keep in mind that the end goal is usually to apply the techniques to solve algebraic equations - as demonstrated in later pages of this module.
Adding or subtracting like terms
You can simplify an algebraic expression by adding or subtracting like terms as follows:
-
Rewrite the expression so that all like terms are next to each other. When you do this, remember to shift the \(+\) or \(–\) sign that is in front of the term with it.
-
Simplify by adding or subtracting like terms.
Example: Simplify the algebraic expression \(2a\,–\,3b\,–\,a\,+\,4ab\,–\,2b\)
Solution: Following the steps above, we have:
-
Rewriting the expression so that all like terms are next to each other gives \(2a\,–\,a\,–\,3b\,–\,2b\,+\,4ab\) (or you can write it in other ways, as long as all the \(a\) terms are together and all the \(b\) terms are together; the \(ab\) term doesn’t have any like terms)
-
Adding and subtracting the like terms in the rearranged algebraic expression \(2a\,–\,a\,–\,3b\,–\,2b\,+\,4ab\) gives \(2a\,–\,a = a\) and \(-3b\,–\,2b = -5b\), so our simplified expression is \(a\,-\,5b\,+\,4ab\)
Multiplying or dividing terms
Note that there are a few different types of notation for indicating that two (or more) terms need to be multiplied together. For example, if \(x\) and \(y\) are required to be multiplied then this might be specified as \(x \times y\), as \(x.y\), as \((x)(y)\) or as \(x(y)\).
Regardless of how the multiplication is indicated, you can simplify an algebraic expression by multiplying or dividing terms as follows:
-
Rewrite the expression (or each part of the expression, for division) as a product of its factors.
-
If necessary, rewrite the expression (or each part of the expression, for division) so that all the like terms are next to each other.
-
Multiply/divide the constants and multiply/divide the variables, as appropriate. When you do this, don’t forget that when a negative is multiplied (or divided) by a negative, the result is positive (e.g. \(-2 \times -2 = 4\)).
Example 1: Simplify the algebraic expression \(4ab \times 3acd\)
Solution: Following the steps above, we have:
-
Rewriting the expression as a product of its factors gives \(4 \times a \times b \times 3 \times a \times c \times d\)
-
Rewriting the expression so that the like terms are next to each other gives \(4 \times 3 \times a \times a \times b \times c \times d\)
-
Since \(4 \times 3 = 12\) and \(a \times a = a^2\), it follows that the simplified expression is \(12a^2bcd\)
Note that \(a^2\) is an example of an exponent (otherwise known as an indice or power). If you are unsure of how to work with exponents, it is recommended that you visit the Exponents page of this module before proceeding with further examples on this page.
Example 2: Simplify the algebraic expression \(\frac{20x^3y}{4x^2y^2}\)
Solution: Following the steps above, we have:
-
Rewriting each part of the expression as a product of its factors gives \(\frac{20 \times x \times x \times x \times y}{4 \times x \times x \times y \times y}\)
-
The like terms are already next to each other for both parts of this expression, so rewriting is not required
-
Since \(\frac{20}{4} = 5\) and \(\frac{x \times x \times x}{x \times x} = x\) and \(\frac{y}{y \times y} = \frac{1}{y}\), it follows that the simplified expression is \(\frac{5x}{y}\)
Note that the above division above has been performed by simplifying fractions, which works in the same way for variables as it does for constants. If you would like a refresher on how simplifying fractions works, please visit the Fractions section of the Numeracy fundamentals module.
Once you have worked through the examples above, have a go at simplifying some or all of the following algebraic expressions (again, please visit the Exponents page of this module first if required):
ANSWER: This expression contains all like terms, which can be added and subtracted to give \(4c\)
ANSWER: Rearranging this expression gives \(3d - d - 5c + 3c + 4 - 9\), which can then be simplified to \(2d - 2c -5\)
ANSWER: Rewriting this expression gives \(13 \times a \times 2 \times b\), which then gives \(13 \times 2 \times a \times b\) and therefore simplifies to \(26ab\)
ANSWER: Rewriting this expression gives \(\frac{10 \times a \times a \times b}{5 \times a \times c}\), and since \(\frac{10}{5} = 2\) and \(\frac{a \times a}{a} = a\), it follows that it simplifies to \(\frac{2ab}{c}\)
ANSWER: Rearranging this expression gives \(3a - a + b - 3b\), which can then be simplified to \(2a - 2b\)
ANSWER: Rearranging this expression gives \(2f + 3h + 5h - g + g\), which can then be simplified to \(2f + 8h\)
ANSWER: Rearranging this expression gives \(20c + 5c - 4d - 15d + 10\), which can then be simplified to \(25c - 19d + 10\)
ANSWER: Rearranging this expression gives \(-5f + 10f + 102g + 6 + 3\), which can then be simplified to \(5f + 102g + 9\)
ANSWER: Rewriting this expression gives \(4 \times c \times a \times b \times 9\), which then gives \(4 \times 9 \times c \times a \times b\) and therefore simplifies to \(36abc\) (while the variables can be listed in any order, the usual convention is to list them alphabetically)
ANSWER: Rewriting this expression gives \(2 \times a \times a \times 5 \times a \times a\), which then gives \(2 \times 5 \times a \times a \times a \times a\) and therefore simplifies to \(10a^4\)
ANSWER: Rewriting this expression gives \(\frac{12 \times a \times c}{a \times b}\), and since \(\frac{a}{a} = 1\), it follows that it simplifies to \(\frac{12c}{b}\)
ANSWER: Rewriting this expression gives \(\frac{20 \times d \times d \times e \times f}{5 \times d \times e}\), and since \(\frac{20}{5} = 4\) and \(\frac{d \times d}{d} = d\) and \(\frac{e}{e} = 1\), it follows that it simplifies to \(4df\)
Expanding brackets
Often an algebraic expression or equation contains brackets. When this is the case for an equation, sometimes it can be helpful to expand them in order to solve it. This section details how to do this for both one and two sets of brackets (note again that the examples refer to algebraic expressions rather than equations for simplicity; applying the techniques as part of solving algebraic equations will be demonstrated in later pages of this module).
Expanding one set of brackets
An algebraic expression consisting of a term outside one set of brackets can be expanded as follows:
-
Write out each of the multiplications you need to perform, by putting the term outside the brackets together with each term inside the brackets. If you use the multiplication notation of putting brackets around each term when you do this, then you can simply add each pair of terms together and deal with any negative signs later.
-
Perform each of the required multiplications, using the method described previously, again leaving each result in brackets in order to keep track of any negative signs. These will be dealt with next.
-
Remove the brackets from each term, replacing a positive sign with a negative sign if there is one inside the corresponding set of brackets.
Example: Expand the brackets in the algebraic expression \(-3a(2b + 4a - 9)\)
Solution: Following the steps above, we have:
-
Writing out the multiplications we need to perform, using brackets to indicate multiplication and adding each pair of terms, gives \((-3a)(2b) + (-3a)(4a) + (-3a)(-9)\)
-
Performing the multiplication above, keeping the results in brackets, gives \((-6ab) + (-12a^2) + (27a)\)
-
Removing brackets and making the required terms negative gives \(-6ab - 12a^2 + 27a\)
Note that \(a^2\) is an example of an exponent (otherwise known as an indice or power). If you are unsure of how to work with exponents, it is recommended that you visit the Exponents page of this module before proceeding with further examples on this page.
Expanding pairs of brackets
An algebraic expression consisting of two sets of brackets that are being multiplied together can be expanded as follows:
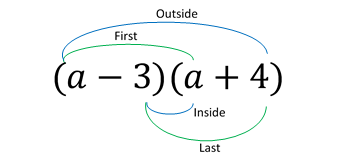
- Write out each of the multiplications you need to perform, by putting each term in the first set of brackets with each term in the second set of brackets and adding these terms together. Again, use brackets to indicate multiplication and add each pair of terms to avoid any confusion with negative signs. Note that a handy way of remembering which terms to multiply when there are two terms in each set of brackets is with the acronym FOIL, which stands for:
- First: Multiply the first terms in each bracket
- Outside: Multiply the two outside terms
- Inside: Multiply the two inside terms
-
Last: Multiply the last terms in each bracket
\(\)
-
Perform each of the required multiplications, leaving each result in brackets in order to keep track of any negative signs. These will be dealt with in the next step.
-
Remove the brackets from each term, replacing the positive sign with a negative sign if there is one inside the corresponding set of brackets.
- Simplify the expression by adding and/or subtracting like terms as required (as detailed in the above section).
Example: Expand the brackets in the algebraic expression \((a - 3)(a + 4)\)
Solution: Following the steps above, we have:
-
Writing out the multiplications we need to perform, using brackets to indicate multiplication and adding each pair of terms, gives \((a)(a) + (a)(4) + (-3)(a) + (-3)(4)\)
Again note that FOIL can help with this:
-
Performing the multiplication above, keeping the results in brackets, gives \((a^2) + (4a) + (-3a) + (-12)\)
-
Removing brackets and making the required terms negative gives \(a^2 + 4a - 3a - 12\)
-
Finally, simplifying the expression gives \(a^2 + a - 12\)
Once you have worked through the examples above, have a go at expanding brackets in the following algebraic expressions (again, please visit the Exponents page of this module first if required):
\(= (b)(3) + (b)(b)\)
\(= 3b + b^2\)
\(= (3xy)(6x) + (3xy)(-y^2) + (3xy)(x^2y)\)
\(= 18x^2y) + (-3xy^3) + (3x^3y^2)\)
\(= 18x^2y - 3xy^3 + 3x^3y^2\)
\(= (e)(g) + (e)(f) + (f)(g) + (f)(f)\)
\(= eg + ef + fg + f^2\)
\(= (c)(-c) + (c)(-3d) + (-4d)(-c) + (-4d)(-3d)\)
\(= (-c^2) + (-3cd) + (4cd) + (12d^2)\)
\(= -c^2 - 3cd + 4cd + 12d^2\)
\(= -c^2 + cd + 12d^2\)
\(= (a)(-a) + (a)(1) + (a)(-ac^2)\)
\(= (-a^2) + (a) + (-a^2c^2)\)
\(= -a^2 + a - a^2c^2\)
\(= (-3d)(3) + (-3d)(-2c) + (-3d)(5d)\)
\(= (-9d) + (6cd) + (-15d^2)\)
\(= -9d + 6cd - 15d^2\)
\(= (-a^3)(-a^2) + (-a^3)(-3a) + (-a^3)(4)\)
\(= (a^5) + (3a^4) + (-4a^3)\)
\(= a^5 + 3a^4 - 4a^3\)
\(= (4dg^2)(2d) + (4dg^2)(3g^3)\)
\(= 8d^2g^2 + 12dg^5\)
\(= (7x)(8x) + (7x)(-3y) + (2y)(8x) + (2y)(-3y)\)
\(= (56x^2) + (-21xy) + (16xy) + (-6y^2)\)
\(= 56x^2 - 21xy + 16xy - 6y^2\)
\(= 56x^2 - 5xy - 6y^2\)
\(=(x^2)(x) + (x^2)(y) + (y)(x) + (y)(y)\)
\(= x^3 + x^2y + xy + y^2\)
\(= (x)(2x) + (x)(-4) + (3y)(2x) + (3y)(-4)\)
\(= (2x^2) + (-4x) + (6xy) + (-12y)\)
\(= 2x^2 - 4x + 6xy - 12y\)
\(= (2x)(2x) + (2x)(-1) + (3)(2x) + (3)(-1)\)
\(= (4x^2) + (-2x) + (6x) + (-3)\)
\(= 4x^2 - 2x + 6x - 3\)
\(= 4x^2 + 4x - 3\)
Factorising
Factorising is essentially the opposite of expanding brackets; instead of removing brackets, you put them into an algebraic expression or equation. Factorising is another tool that you can use to help you solve algebraic equations in certain situations (although obviously, it wouldn’t help to go back and forth expanding and factorising the same equation!).
This section details how to factorise using one set of brackets, and at a common example of factorising using two sets of brackets (note again that the examples refer to algebraic expressions rather than equations for simplicity; applying the techniques as part of solving algebraic equations will be demonstrated in later pages of this module).
Factorising with one set of brackets
You can factorise an algebraic expression using one set of brackets as follows:
-
Identify the highest common factor for all terms in the expression (where the highest common factor is the largest term that divides into each term in the expression). This may be a constant or a variable or variables, or a combination of both.
-
Put the highest common factor outside of a set of brackets.
-
Put what remains of each term in the original expression inside the brackets.
Example: Factorise the algebraic expression \(3x^2 + 21x\)
Solution: Following the steps above, we have:
-
The highest common factor is \(3x\), since \(3\) divides into each term in the expression a whole number of times and there is one \(x\) in each term.
-
Putting this outside a set of brackets gives \(3x(…..)\)
-
Since there is an \(x\) remaining in \(3x^2\) when it is divided through by \(3x\), the first term inside the brackets should be \(x\).
Since there is a \(7\) remaining in \(21x\) when it is divided through by \(3x\), the second term inside the brackets should be \(7\).
Therefore it follows that the factorised form of the expression is \(3x(x + 7)\)
Note that \(x^2\) is an example of an exponent (otherwise known as an indice or power). If you are unsure of how to work with exponents, it is recommended that you visit the Exponents page of this module before proceeding with further examples on this page.
Factorising with two sets of brackets
Sometimes two sets of brackets are required to factorise an expression. A common example of this is when factorising a quadratic, which is an algebraic expression of the form \(ax^2 + bx + c\) (where \(a\), \(b\) and \(c\) are numbers, and \(a\) does not equal 0 - as this would not be a quadratic).
For more information on quadratic equations see the Solving quadratic equations page of this module, but in the meantime know that you can factorise a quadratic equation for which \(a = 1\) as follows:
-
Write two sets of brackets, and put the variable used in the expression inside both.
-
Determine pairs of factors for the last term in the expression, taking into account whether these factors are positive or negative.
-
Determine which of these pairs of factors can be added together or subtracted from one another to give the constant associated with the middle term in the expression. Then write one of these in each of the sets of brackets, being sure to use appropriate signs.
Example: Factorise the algebraic expression \(x^2 + 7x + 12\)
Solution: Following the steps above, we have:
-
Writing out two sets of brackets with the variable inside each gives \((x\textrm{…..})(x\textrm{…..})\)
-
The pairs of factors for \(12\) are \(1\) and \(12\), \(2\) and \(6\) and \(3\) and \(4\). Note that both terms must be positive, since they need to multiply together to make positive \(12\) and add together to make positive \(7\)
-
The pair of factors that can be added together to make \(7\) is \(3\) and \(4\), so the factorised form of \(x^2 + 7x + 12\) is \((x + 3)(x + 4)\), or \((x + 4)(x + 3)\) (it doesn’t matter which way around you write it)
Once you have worked through the examples above, have a go at factorising the following algebraic expressions (again, please visit the Exponents page of this module first if required):
Common factor is \(2a\), so factorising gives \(2a(7 + 4b)\)
Common factor is \(3x^2y\), so factorising gives \(3x^2y(4x - y + 2z)\)
This is a quadratic so we need two sets of brackets, and two numbers that multiply together to make \(-12\) and add together to make \(1\) (since \(x = 1x\)). The factors of \(12\) are \(1\) & \(12\), \(2\) & \(6\) and \(3\) & \(4\), and one of each pair must be negative and one positive in order to multiply together to make \(-12\). The correct pair is \(-3\) and \(4\), since \(-3 + 4 = 1\), so the expression can be factorised as \((x - 3)(x + 4)\)
This is a quadratic so we need two sets of brackets, and two numbers that multiply together to make \(12\) and add together to make \(-8\). The factors of \(12\) are \(1\) & \(12\), \(2\) & \(6\) and \(3\) & \(4\), and both numbers must be negative in order to multiply together to make \(12\) and add together to make \(-8\). The correct pair is \(-2\) and \(-6\), since \(-2 - 6 = -8\), so the expression can be factorised as \((y - 2)(y - 6)\)
This is a quadratic so we need two sets of brackets, and two numbers that multiply together to make \(-12\) and add together to make \(-4\). The factors of \(12\) are \(1\) & \(12\), \(2\) & \(6\) and \(3\) & \(4\), and one of each pair must be negative and one positive in order to multiply together to make \(-12\). The correct pair is \(2\) and \(-6\), since \(2 - 6 = -4\), so the expression can be factorised as \((z + 2)(z - 6)\)
Common factor is \(5c\), so factorising gives \(5c(2 + 3c)\)
Common factor is \(4ac\), so factorising gives \(4ac(4b + 1 - 3bc)\)
Common factor is \(3m\), so factorising gives \(3m(n + 2m - 4n^2)\)
Common factor is \(-5x^2\), so factorising gives \(-5x^2(y + 2x + 4)\)
This is a quadratic so we need two sets of brackets, and two numbers that multiply together to make \(6\) and add together to make \(5\). The factors of \(6\) are \(1\) & \(6\) and \(2\) & \(3\), and both numbers must be positive in order to multiply together to make \(6\) and add together to make \(5\). The correct pair is \(2\) and \(3\), since \(2 + 3 = 5\), so the expression can be factorised as \((x + 2)(x + 3)\)
This is a quadratic so we need two sets of brackets, and two numbers that multiply together to make \(-10\) and add together to make \(-3\). The factors of \(10\) are \(1\) & \(10\) and \(2\) & \(5\), and one of each pair must be negative and one positive in order to multiply together to make \(-10\). The correct pair is \(2\) and \(-5\), since \(2 - 5 = -3\), so the expression can be factorised as \((y + 2)(y - 5)\)
This is a quadratic so we need two sets of brackets, and two numbers that multiply together to make \(24\) and add together to make \(-10\). The factors of \(24\) are \(1\) & \(24\), \(2\) & \(12\), \(3\) & \(8\) and \(4\) & \(6\), and both numbers must be negative in order to multiply together to make \(24\) and add together to make \(-10\). The correct pair is \(-6\) and \(-4\), since \(-6 - 4 = -10\), so the expression can be factorised as \((a - 6)(a - 4)\)
This is a quadratic so we need two sets of brackets, and two numbers that multiply together to make \(-20\) and add together to make \(-1\). The factors of \(20\) are \(1\) & \(20\), \(2\) & \(10\) and \(4\) & \(5\), and one of each pair must be negative and one positive in order to multiply together to make \(-20\). The correct pair is \(4\) and \(-5\), since \(4 - 5 = -1\), so the expression can be factorised as \((b + 4)(b - 5)\)
This is a quadratic so we need two sets of brackets, and two numbers that multiply together to make \(1\) and add together to make \(2\). The only factors of \(1\) are \(1\) & \(1\), and we need both of these to be positive in order to multiply together to make \(1\) and add together to make \(2\). Hence the expression can be factorised as \((c + 1)(c + 1)\), which we would usually write as \((c + 1)^2\)
This is a quadratic so we need two sets of brackets, and two numbers that multiply together to make \(-30\) and add together to make \(1\). The factors of \(30\) are \(1\) & \(30\), \(2\) & \(15\), \(3\) & \(10\) and \(5\) & \(6\), and one of each pair must be negative and one positive in order to multiply together to make \(-30\). The correct pair is \(6\) and \(-5\), since \(6 - 5 = 1\), so the expression can be factorised as \((d + 6)(d - 5)\)