Introduction to calculus
In calculus, we commonly encounter two different types of quantities: scalars and vectors.
Scalar quantities are those that can be described by their magnitude (or size) alone, and are therefore represented by single numbers. For example, if we say it is \(30^{\circ} C\) outside, we have a pretty clear idea of how warm the weather is. Other examples of scalar quantities are \(40\textrm{km/hr}\), \(5\textrm{kg}\) and \(15\textrm{minutes.}\) This is because speed, mass, and time are all scalar quantities. In other words, scalars only tell us “how much” without including any kind of direction.
Vectors are quantities that have both a magnitude and a direction. For example, if we say a car is travelling at \(60\textrm{km/hr}\) to the north, or that someone has moved \(5\textrm{m}\) to the right, these are vector quantities as we are providing both a magnitude and a direction.
This page looks at how to perform various calculations involving vectors. First, though, we look at how to represent and label vectors in diagrams.
Vector diagrams
A vector can be represented in a diagram as an arrow between two points, with the length of the arrow indicating the magnitude, and the direction it points showing where it is headed. We can then label the vector using either a single lower case letter, usually in bold, or using the names of the points at either end with an arrow above. For example, the vector shown below in green is going from A (its initial point) to B (its terminal point) and could be labelled as \(\mathbf{a}\) or as \(\overrightarrow{AB}.\)
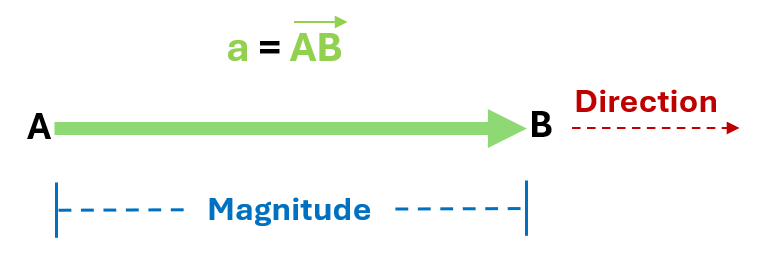
If two vectors have the same magnitude and direction they are called equivalent or equal vectors.
We can add vectors together on a diagram using the nose to tail method (also known as the triangle law).
The nose to tail method says that if two vectors are positioned so that the initial point of one is at the terminal point of another, then we can add the two vectors together to get the displacement vector.
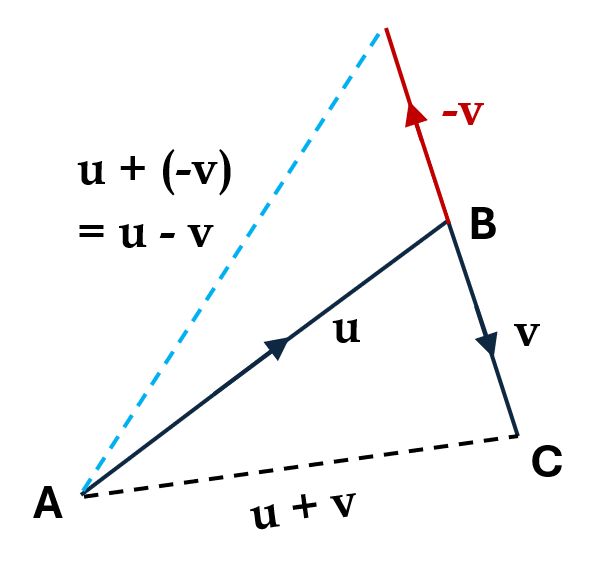
Example: Suppose a person has walked from point A to point B, then changed direction and walked from point B to another point, C:
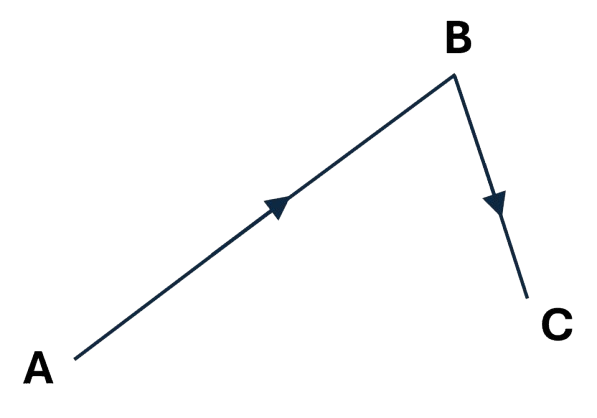
If we label these vectors \(\mathbf{u}\) and \(\mathbf{v}\), where \(\mathbf{u} = \overrightarrow{AB}\) and \(\mathbf{v} = \overrightarrow{BC},\) what is the displacement vector indicating the distance and direction the person is from their starting point?
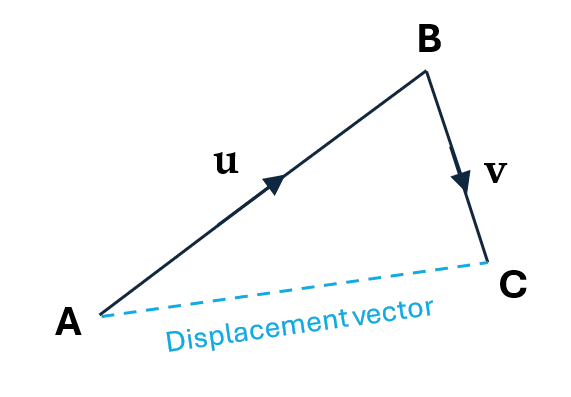
Solution: Since the initial point of \(\mathbf{v}\) is at the terminal point of \(\mathbf{u}\), our displacement vector will be \(\mathbf{u} + \mathbf{v}\)
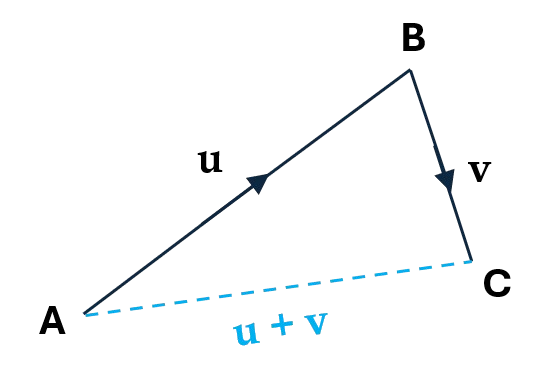
Subtracting vectors on a diagram is done in a similar way. All we need to do is reverse the direction of the vector we want to subtract, and then add as normal. This however means that the addition becomes a subtraction since we would have \(\mathbf{u} + (-\mathbf{v})\) which is the same as \(\mathbf{u} - \mathbf{v}\).
Components
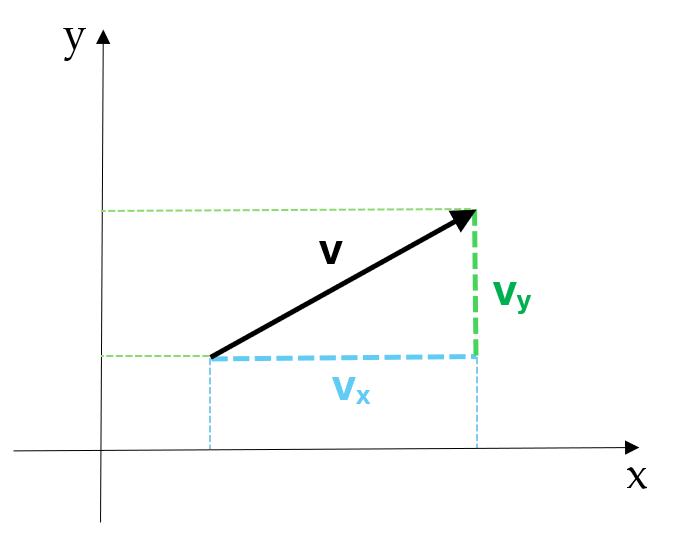
It can be difficult to represent vectors accurately using diagrams, and therefore they are generally written using coordinates in order to actually perform calculations. One way of doing this is to split a vector into parts by looking at its \(x\) and \(y\) components, otherwise known as the Cartesian coordinates (for more on this, and on using polar coordinates instead, see converting between coordinates). A vector’s \(x\) component is how many units ‘long’ it is in relation to the \(x\)-axis, and its \(y\) component is how many units ‘high’ it is in relation to the \(y\)-axis.
If we have vector \(\mathbf{v}\), its components can be written as \(\mathbf{v_x}\) and \(\mathbf{v_y}\). These components are then expressed in the form \(\mathbf{v}=(\mathbf{v}_x, \mathbf{v}_y),\) similar to the coordinates of a graph, or as \(\begin{pmatrix} \mathbf{v}_x \\ \mathbf{v}_y \end{pmatrix}\)
Example:
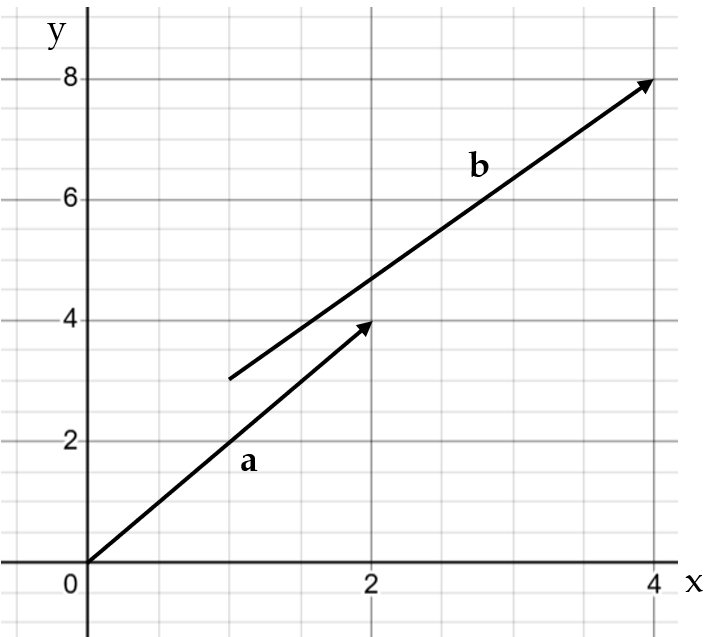
What are the components of the vectors shown below?
Solution:
Vector \(\mathbf{a}\) begins at \((0,0)\) and ends at \((2,4)\) therefore we have \(\mathbf{a} = (2,4)\)
Vector \(\mathbf{b}\) begins at \((1,3)\) and ends at \((4,8)\). To find the components of \(\mathbf{b}\), we first have to find the difference between the coordinates of these points:
\[\begin{aligned} \mathbf{b}_x &= 4 - 1 \\\ &= 3 \\\ \mathbf{b}_y &= 8 - 3 \\\ &= 5 \\\ \end {aligned}\]Therefore, the components for \(\mathbf{b}\) will be \(\mathbf{b} = (3,5)\)
Adding and subtracting vectors
Once we write vectors using components, in order to add or subtract them all we need to do is add or subtract the respective \(x\) and \(y\) components to find the components of the new vector.
Example:
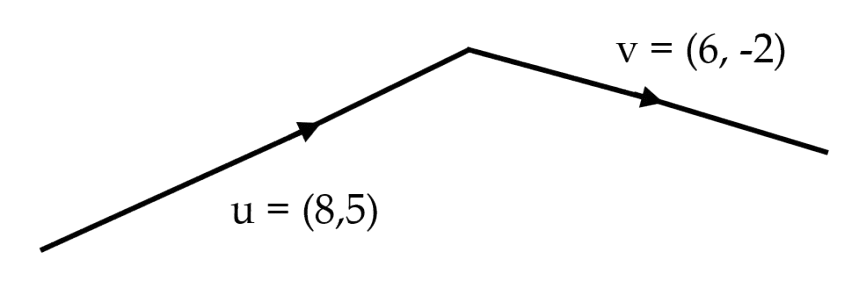
Add the two vectors below to find the displacement vector:
Solution:
The displacement vector’s components will be:
\[\begin{aligned} \mathbf{u} + \mathbf{v} &= (8+6,\,5+(-2)) \\\ &=(14,\,3) \\\ \end{aligned}\]Check your understanding of adding and subtracting vectors by working through the questions below:
\(\begin{aligned} \mathbf{a} + \mathbf{b} &= (3 + 4,\,5+(-7))\\\ &= (7, -2) \\\ \end{aligned}\)
\(\begin{aligned} \mathbf{c} - \mathbf{d} &= (12 - 7, -3 - 2)\\\ &= (5, -5) \\\ \end{aligned}\)
\(\begin{aligned} \mathbf{y} - \mathbf{x} + \mathbf{z} &= (8 - 2 + 7, -3 - 3 + 4)\\\ &= (13, -2) \\\ \end{aligned}\)
Magnitude of a vector
As we know, vectors have both a magnitude and a direction. If we have a vector \(\mathbf{u}\), the magnitude of that vector is written as \(\vert \mathbf{u} \vert,\) or sometimes as \(\Vert \mathbf{u} \Vert\) so that it isn’t confused with the symbol for absolute value.
The magnitude of a vector is different to the components of a vector, as the magnitude is the numeric value of the vector. However, we can find the magnitude of a vector given its components using Pythagoras’ theorem.
The magnitude of a vector \(\mathbf{u} = (\mathbf{u}_x , \mathbf{u}_y)\) will be:
\[\vert \mathbf{u} \vert = \sqrt{\mathbf{u_x}^2 + \mathbf{u_y}^2}\]Example:
Find the magnitude of \(\mathbf{v} = (6,\,8)\)
Solution:
\[\begin{aligned} \vert \mathbf{v} \vert &= \sqrt{\mathbf{v_x}^2 + \mathbf{v_y}^2} \\\ &= \sqrt{6^2 + 8^2} \\\ &= \sqrt{100} \\\ &= 10 \\\ \end{aligned}\]Unit vectors
If a vector has a magnitude of \(1\) it is called a unit vector. There are two commonly known unit vectors that are often used in vector notation. The unit vectors are \(\mathbf{i}\) and \(\mathbf{j}\) and they sit along the \(x\) and \(y\) axes, respectively:
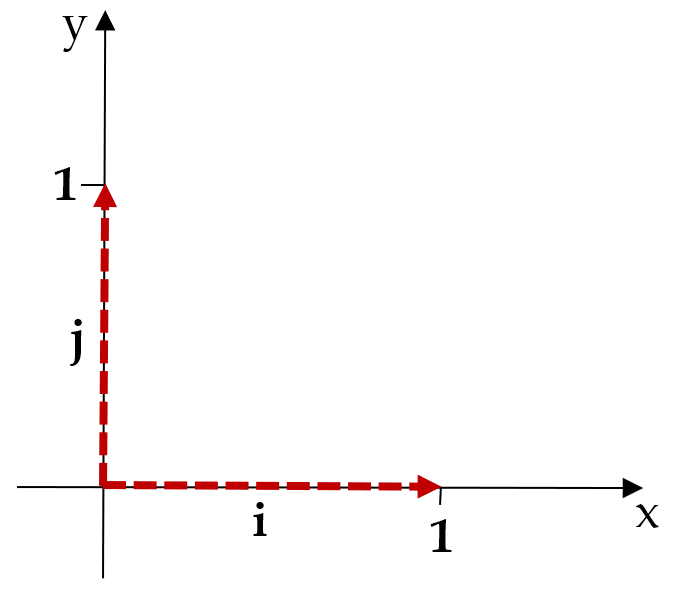
Vectors can also be represented using these unit vectors, for example as \(\mathbf{v} = x\mathbf{i} + y\mathbf{j}\)
Check your understanding of the magnitude of vectors and unit vector notation by working through the questions below:
\(\begin{aligned} \vert \mathbf{a} \vert &= \sqrt{\mathbf{a_x}^2 + \mathbf{a_y}^2} \\\ &= \sqrt{4^2 + (-3)^2} \\\ &= \sqrt{25} \\\ &= 5 \\\ \end{aligned}\)
\(\begin{aligned} \vert \mathbf{b} \vert &= \sqrt{\mathbf{b_x}^2 + \mathbf{b_y}^2} \\\ &= \sqrt{(-7)^2 + 5^2} \\\ &= \sqrt{74} \\\ &= 8.602 \\\ \end{aligned}\)
\(\begin{aligned} \vert \mathbf{c} \vert &= \sqrt{\mathbf{c_x}^2 + \mathbf{c_y}^2} \\\ &= \sqrt{4^2 + (-2)^2} \\\ &= \sqrt{20} \\\ &= 4.47 \\\ \end{aligned}\)
Scalar multiples
Vectors can be multiplied by scalar quantities in order to scale them up or down. To multiply a vector by a scalar, all we need to do is multiply each of the vector’s components by the scalar.
If we have a vector \(\mathbf{u}\), the scaled vector will be \(k\mathbf{u}\) where \(k\) is the scalar and \(\mathbf{u}\) is the vector.
Example 1:
Multiply the vector \(\mathbf{f} = (9,3)\) by \(4\)
Solution:
\[\begin{aligned} 4 \mathbf{f} &= (4 \times 9 ,\,4 \times 3) \\\ &= (36, 12) \\\ \end{aligned}\]Example 2:
Calculate \(2.5 \mathbf{u}\) when \(\mathbf{u} = (5, 8)\)
Solution:
\[\begin{aligned} 2.5 \mathbf{u} &= (2.5 \times 5,\,2.5 \times 8) \\\ &= (12.5, 20) \\\ \end{aligned}\]Check your understanding of calculating scalar multiples by working through the questions below:
\(\begin{aligned} 3 \mathbf{a} &= (3 \times 7,\,3 \times -6) \\\ &= (21, -18) \\\ \end{aligned}\)
\(\begin{aligned} 7 \mathbf{b} &= (7 \times -3) \mathbf{i} + (7 \times 4) \mathbf{j} \\\ &= -21 \mathbf{i} + 28 \mathbf{j} \\\ \end{aligned}\)
\(\begin{aligned} 3 \mathbf{c} - 4 \mathbf{d} &= (3 \times 12 - 4 \times (-3)) \mathbf{i} + (3 \times 3 - 4 \times 5) \mathbf{j} \\\ &= (36 + 12) \mathbf{i} + (9 - 20) \mathbf{j} \\\ &= 48 \mathbf{i} - 11 \mathbf{j} \\\ \end{aligned}\)
Converting between coordinates
So far we have been using Cartesian coordinates to express vectors in terms of their \(x\) and \(y\) components, but they can also be expressed using polar coordinates. This is when we state the magnitude and direction instead (note that the direction is stated using an angle either in degrees or in radians - we will use degrees here). For example, we could write a vector \(\mathbf{v}\) as \((12, 30^\circ)\) using polar coordinates.
To convert between Cartesian and polar coordinates we need to use trigonometry. In particular, to convert from Cartesian coordinates to polar coordinates we use Pythagoras’ theorem to calculate the magnitude and the tangent trigonometric ratio to calculate the direction.
To write the vector \(\mathbf{a} = (\mathbf{a}_x, \mathbf{a}_y)\) using polar coordinates \((r, \theta)\) we calculate:
\[r = \sqrt{\mathbf{a_x}^2 + \mathbf{a_y}^2}\] \[\theta = \tan^{-1}\frac{a_y}{a_x}\]Example:
Write \(\mathbf{a} = (10, 4)\) using polar coordinates rounded to two decimal places.
Solution:
\[\begin{aligned} r &= \sqrt{\mathbf{a_x}^2 + \mathbf{a_y}^2} \\\ &= \sqrt{10^2 + 4^2} \\\ &= \sqrt{116} \\\ &= 10.77 \\\ \end{aligned}\] \[\begin{aligned} \theta &= \tan^{-1}\frac{a_y}{a_x} \\\ &= \tan^{-1}\frac{4}{10} \\\ &= 21.80^\circ \end{aligned}\]Therefore \(\mathbf{a} = (10.77,\,21.80^\circ)\)
To convert from polar coordinates to Cartesian coordinates we use the sine and cosine trigonometric ratios.
To write the vector \(\mathbf{b} = (r, \theta)\) using Cartesian coordinates \((\mathbf{b}_x, \mathbf{b}_y)\) we calculate:
\[\mathbf{b}_x = r\,cos\,\theta\] \[\mathbf{b}_y = r\,sin\,\theta\]Example:
Write \(\mathbf{b} = (25, 30^\circ)\) using Cartesian coordinates rounded to two decimal places.
Solution:
\[\begin{aligned} \mathbf{b}_x &= r\,cos\,\theta \\\ &= 25\,cos\,30^\circ \\\ &= 21.65 \\\ \end{aligned}\] \[\begin{aligned} \mathbf{b}_y &= r\,sin\,\theta \\\ &= 25\,sin\,30^\circ \\\ &= 12.5 \\\ \end{aligned}\]Therefore \(\mathbf{b} = (21.65, 12.5)\)
Check your understanding of how to convert between coordinates by working through the questions below:
Therefore \(\mathbf{u} = (12.37,\,14.04^\circ)\)
Therefore \(\mathbf{v} = (6.36,\,12.47)\)
Therefore the vector can be expressed as \((-2.46\textrm{m},\,1.72\textrm{m})\)
Multiplying vectors
If we want to multiply two vectors together, rather than just multiplying a vector by a scalar, there are two different ways of doing this. One method, known as the dot product, produces a scalar result, while the other method, known as the cross product, produces a vector result. While the cross product is not covered here, how to calculate the dot product is detailed below.
Dot product
The dot product of two vectors \(\mathbf{a}\) and \(\mathbf{b}\) is written as:
\[\mathbf{a} . \mathbf{b}\]This can be calculated in two different ways, depending if the vectors are written using Cartesian or polar coordinates. If the vectors are written using Cartesian coordinates, we multiple the two \(x\) components together and the two \(y\) components together and then add the results.
The dot product of two vectors written using Cartesian coordinates is:
\[\mathbf{a} . \mathbf{b} = \mathbf{a}_x \times \mathbf{b}_x + \mathbf{a}_y \times \mathbf{b}_y\]Example:
Calculate \(\mathbf{a} . \mathbf{b}\) given that \(\mathbf{a} = (-2, 4)\) and \(\mathbf{a} = (3, 5)\)
Solution:
\[\begin{aligned} \mathbf{a} . \mathbf{b} &= \mathbf{a}_x \times \mathbf{b}_x + \mathbf{a}_y \times \mathbf{b}_y \\\ &= -2 \times 3 + 4 \times 5 \\\ &= -6 + 20 \\\ &= 14 \\\ \end{aligned}\]If the vectors are written using polar coordinates, we multiply the magnitude of each vector together and then multiply by the cosine of the angle between them.
The dot product of two vectors written using polar coordinates is:
\[\mathbf{a} . \mathbf{b} = \vert \mathbf{a} \vert \times \vert \mathbf{b} \vert \times cos\,\theta\]where \(\theta\) is the angle between the two vectors.
Example:
Calculate \(\mathbf{a} . \mathbf{b}\) given that \(\mathbf{a} = (4, 45^\circ)\) and \(\mathbf{b} = (7, 105^\circ)\)
Solution:
The angle between the two vectors is \(105^\circ - 45^\circ = 60^\circ,\) so:
\[\begin{aligned} \mathbf{a} . \mathbf{b} &= \vert \mathbf{a} \vert \times \vert \mathbf{b} \vert \times cos\,\theta \\\ &= 4 \times 7 \times cos\,60^\circ \\\ &= 28 \times 0.5 \\\ &= 14 \\\ \end{aligned}\]Check your understanding of using the dot product to multiply vectors by working through the questions below:
The angle between the two vectors is \(75^\circ - 22^\circ = 53^\circ,\) so:
\[\begin{aligned} \mathbf{u} . \mathbf{v} &= \vert \mathbf{u} \vert \times \vert \mathbf{v} \vert \times cos\,\theta \\\ &= 3 \times 8 \times cos\,53^\circ \\\ &= 24 \times 0.602 \\\ &= 14.44 \\\ \end{aligned}\]From question 2 above, we have: \(\mathbf{c} . \mathbf{d} = 33\)
Furthermore, calculating the magnitude of the vectors gives:
\[\begin{aligned} \vert \mathbf{c} \vert &= \sqrt{\mathbf{c_x}^2 + \mathbf{c_y}^2} \\\ &= \sqrt{6^2 + 7^2} \\\ &= \sqrt{85} \\\ &= 9.22 \\\ \end{aligned}\] \[\begin{aligned} \vert \mathbf{d} \vert &= \sqrt{\mathbf{d_x}^2 + \mathbf{d_y}^2} \\\ &= \sqrt{9^2 + (-3)^2} \\\ &= \sqrt{90} \\\ &= 9.49 \\\ \end{aligned}\]So we have:
\[\begin{aligned} \vert \mathbf{u} \vert \times \vert \mathbf{v} \vert \times cos\,\theta &= 33\\\ \therefore 9.22 \times 9.49 \times cos\,\theta &= 33 \\\ \therefore cos\,\theta &= 0.38 \\\ \therefore \theta &= cos^{-1}0.38 \\\ \therefore \theta &= 67.83^\circ \\\ \end{aligned}\]So the angle between the two vectors is \(67.83^\circ\)