Introduction to calculus
The integral of a function is used to find the area under the graph of that function. There are two types of integrals, definite integrals and indefinite integrals. To find the integral of a function we use the rules of integration.
Indefinite integrals can also be called antiderivatives, and integration can be called antidifferentiation. This is because integration is the inverse of differentiation.
Understanding integration
Consider the graph:
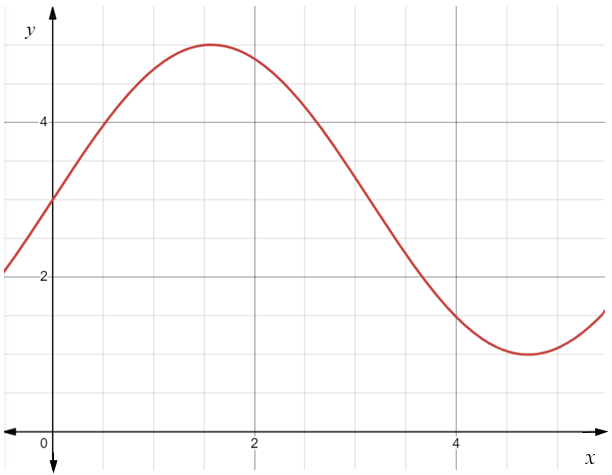
If we wanted to find the area between the graph and the \(x\)-axis we could calculate the function at a few points and add these up, essentially breaking the area up into smaller parts.
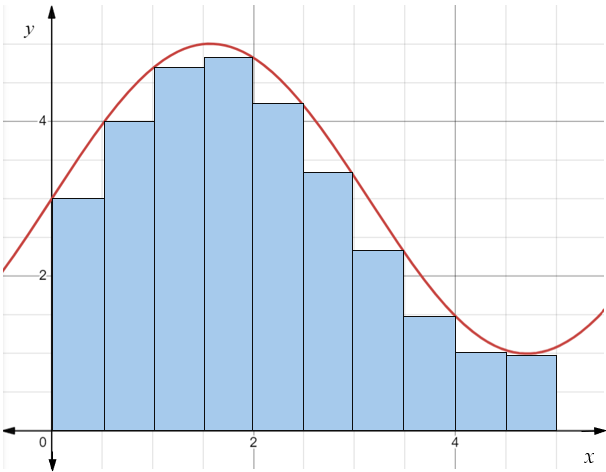
The smaller the parts we use, or the smaller the change in \(x\), the more accurate we can be in our answer. However, this also means more work as there will be an infinite number of parts that could be used to find the area. Instead of doing a lot of individual calculations and adding up all these individual parts, we can use integration to find the integral of the function and use that to calculate the area under the graph.
For example, consider the graph below:
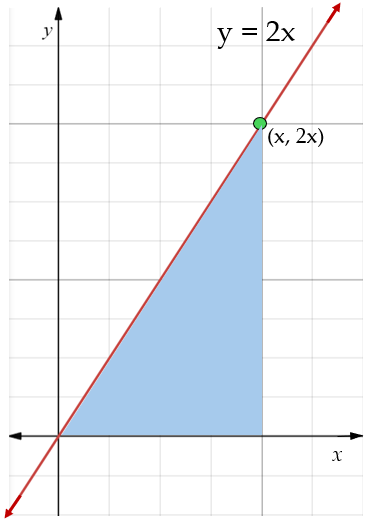
We know that the formula to calculate the area of a triangle is \(\frac 12 base \times height\). In this example, our base is going to be the value of \(x\), and our height will be \(2x\). So we have:
\[\begin{aligned} Area\;under\;the\;graph &= \frac 12 (x)(2x) \\\ &= x^2 \\\ \end{aligned}\]This means that the integral of the function \(y = 2x\) is \(x^2\). You may notice that if we were asked to find the derivative of that integral, the answer would be \(2x\).
Integrals don’t always appear as simple as this example, but that’s why we have rules we can follow to help us integrate any given function.
If we have \(y = f(x)\), the notation for the integral of that function will look like:
\[\int f(x)\,dx\]The \(\int\) is the mathematical integral symbol, and \(dx\) represents the change in \(x\).
This notation is used when finding an indefinite integral.
Definite vs indefinite
An indefinite integral does not have any defined limits. Finding the indefinite integral of a function is the same as finding the antiderivative of that function. Your answer will still look like a function rather than a value, and will be the inverse of the derivative.
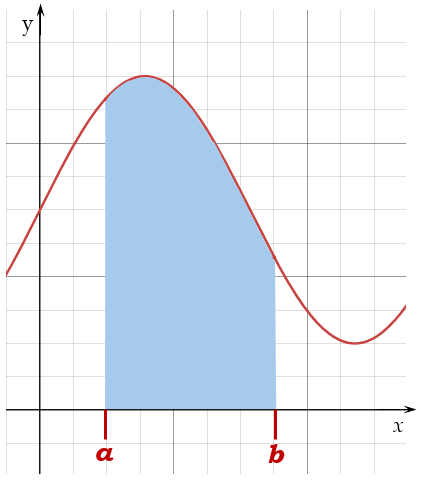
A definite integral has defined upper and lower limits. These are the values of \(x\) between which you are being asked to find the area under the graph.
The notation of a definite integral will have values, or limits, attached to the integral symbol \(\int\):
\[\int_a^b f(x)\,dx\]This is asking us to find the integral of the function \(f(x)\) between \(x=a\) and \(x=b\), that is, the value of the area under the graph between \(x=a\) and \(x=b\):
This is performed by finding the value of the integral at \(x=a\) and subtracting it from the value of the integral at \(x=b\):
\[\int_a^b f(x)\,dx = \int f(b) - \int f(a)\]Note: if you have a negative definite integral, you can make it positive by swapping the limits.
\[- \int_b^a f(x)\,dx = \int_a^b f(x)\,dx\]In general, if you are required to find the integral of a function, you are probably being asked to find the definite integral. If you are required to find the indefinite integral of a function, you may be asked to find the antiderivative and will not be given any limits.
Integration rules
The rules of integration are the inverse of the rules of differentiation. If you’d like to know more about differentiation and how it compares to integration, have a look at our guide to derivatives.
Each of the rules below have the notation expected for indefinite integrals. However, there are also examples for finding definite integrals using each rule.
You’ll notice that each indefinite integral includes a \(+ C\). This is known as the constant of integration. This is added onto the end of indefinite integrals as the derivative of any real constant is zero, and we need to include the possibility that our integral contains a constant. The constant of integration is not required for definite integrals.
Constant rule
The integral of a constant will always be that same constant multiplied by a variable, usually \(x\).
The integral of a constant will be:
\[\int a\;dx\;=\;ax+C\]Example 1:
Find the antiderivative of \(y = 8\)
Solution:
\[\int 8\;dx = 8x + C\]Example 2:
Evaluate the definite integral \(\int_2^5 7\,dx\)
Solution:
\[\begin{aligned} \int_2^5 \,7\,dx &= 7(5) - 7(2) \\\ &= 35 - 14 \\\ &= 21 \\\ \end{aligned}\]Power rule
When finding the integral of a variable with a power, add one to the power and then divide it by that same new power.
The integral of a variable with a power will be:
\[\int x^n\,dx = \frac{x^{n+1}}{n+1} + C\]Example 1:
Find the indefinite integral of \(y=x\)
Solution:
\[\int x\,dx = \frac{x^2}{2} + C\]Example 2:
Find the indefinite integral of \(y=2x^5\)
Solution:
\[\begin{aligned} \int 2x^5\,dx &= \frac{2x^6}{6} + C \\\ &= \frac{x^6}{3} + C \\\ \end{aligned}\]Example 3:
Evaluate \(\int_5^8 2x^2 dx\)
Solution:
\[\begin{aligned} \int_5^8 \,2x^2\,dx &= \frac{2(8)^3}{3} - \frac{2(5)^3}{3} \\\ &= \frac{1024}{3} - \frac{250}{3} \\\ &= 258 \\\ \end{aligned}\]Multiplier constant
If the function is being multiplied by a constant, we can move the constant and place it outside the integration symbol. We can then put it back in front of our integrated function. Let’s have a look at some of the examples from above and see if we get the same results using the multiplier constant rule.
Example 1:
Find the indefinite integral of \(y=2x^5\)
Solution:
We want to find \(\int 2x^5\,dx\), but let’s move the constant first.
\[2 \int x^5\,dx\]Now, we can find the integral of our function, and multiply it by our constant, \(2\), again.
\[\begin{aligned} 2 \int x^5\,dx &= 2 \frac{x^6}{6} + C \\\ &= \frac{x^6}{3} + C \\\ \end{aligned}\]Example 2:
Evaluate \(\int_5^8 2x^2 dx\)
Solution:
Again, we can first move the multiplier constant outside of the integration.
\[\begin{aligned} 2\,\int_5^8 \,x^2\,dx &= 2 (\frac{(8)^3}{3} - \frac{(5)^3}{3}) \\\ &= 2 (\frac{512}{3} - \frac{125}{3}) \\\ &= 2(129) \\\ &= 258 \\\ \end{aligned}\]As you can see, using the multiplier constant rule gives the same answer for the examples that we saw while trying out the power rule above. These examples were just to demonstrate that it worked and while it may not always be necessary to use the multiplier constant rule, it’s good to know it is an option when integrating functions as it can assist in solving more difficult integrals, such as when having to use integration by substitution.
Trigonometric functions
We can also find the integral of the trigonometric functions \(sin\), \(cos\), and \(tan\). It’s important to note that when working with the integrals of trigonometric functions, \(x\) will be in radians.
The integral of \(sin\) is \(-cos\):
\[\int sin\,x\,dx = -cos\,x + C\]The integral of \(cos\) is \(sin\):
\[\int cos\,x\,dx = sin\,x + C\]The integral of \(tan\) is a little more complicated, due to the nature of the graph of \(y = tan\,x\). To find the integral of \(tan\) you need to use integration by substitution. This will give you the following (where \(\vert sec\,x \vert\) represents the absolute value of \(sec\,x\) , which is its non-negative value):
\[\int tan\,x\,dx = ln\,|sec\,x|\, + C\]Example 1:
Find \(\int 3\,sin\,x\,dx\)
Solution:
\[\begin{aligned} \int 3\,sin\,x\,dx &= 3\,\int sin\,x\,dx \\\ &= - 3\,cos\,x + C \\\ \end{aligned}\]Example 2:
Evaluate \(\int_0^{\pi} 2\,sin\,x\,dx\)
Solution:
\[\begin{aligned} \int_0^{\pi} 2\,sin\,x\,dx &= 2 \int_0^{\pi} sin\,x\,dx \\\ &= 2(- cos\,\pi - (-cos\,0)) \\\ &= 2(1 + 1) \\\ &= 4 \\\ \end{aligned}\]Euler’s number
We can also find the integral of \(e^x\). We can easily find the integral of \(e\), even when \(x\) has a coefficient. If \(x\) has its own power, we need to start using imaginary numbers, and that is not covered in this module.
The integral of \(e^x\) is \(e^x\):
\[\int e^x\,dx = e^x + C\]When \(x\) has a coefficient, we divide the answer by this number:
\[\int e^{ax}\,dx = \frac{e^{ax}}{a} + C\]Finally, we can use exponent laws to expand this one step further as follows:
\[\int e^{ax + b}\,dx = \frac{e^{ax + b}}{a} + C\]Example 1:
Determine the integral of
\[\int e^{3x+2}\,dx\]Solution:
\[\int e^{3x+2}\,dx = \frac{e^{3x+2}}{3} + C\]Example 2:
Evaluate the integral
\[\int_2^3 e^{3x}\,dx\]Solution:
\[\begin{aligned} \int_2^3 e^{3x}\,dx &= \frac{e^{3(3)}}{3} - \frac{e^{3(2)}}{3} \\\ &= 2701.03 - 134.48 \\\ &= 2566.55 \end{aligned}\]Logarithms
We can find the integral of logarithms with various bases, however as the natural log \(ln\) (the log with base \(e\), so \(log_e\)) is more frequently used in calculus it is the only one covered here.
The integral of the natural log, \(ln\,x,\) is:
\[\int ln\,x\,dx = x\,ln\,x - x + C\]or
\[\int ln\,x\,dx = x\,(ln\,x - 1) + C\]Example 1:
Find the antiderivative of \(f(x) = ln\,(2x)\)
Solution:
Using the logarithm laws we know that \(ln\,(2x) = ln\,x + ln\,2\)
\[\begin{aligned} \therefore \quad \int ln\,2x\,dx &= \int (ln\,x + ln\,2)\,dx \\\ &= \int ln\,x\,dx + \int ln\,2\,dx \\\ &= x\,ln\,x - x + x\,ln\,2 + C \\\ \end{aligned}\]Example 2:
Calculate the integral below to 3 decimal places.
\[\int_1^3 \frac{1}{2} ln\,x\,dx\]Solution:
\[\begin{aligned} \int_1^3 \frac{1}{2} ln\,x\,dx &= \frac{1}{2} \int_1^3 ln\,x\,dx \\\ &= \frac{1}{2}((3\,ln\,3 - 3) - (ln\,1 - 1)) \\\ &= \frac{1}{2}((3\,ln\,3 - 3) - (-1)) \\\ &= \frac{1}{2}(3\,ln\,3 - 2) \\\ &= 0.648 \\\ \end{aligned}\]Reciprocals
Now that we’ve had a look at logarithms, it’s important to have a look at the integral of reciprocals. A reciprocal is also known as a (multiplicative) inverse. For example, the inverse of \(2\) is \(\frac{1}{2},\) and the inverse of \(x\) is \(\frac{1}{x}\) (this is known as the reciprocal function).
The integral of the reciprocal function is as follows (where \(\vert x \vert\) represents the absolute value of \(x\) , which is its non-negative value):
\[\int \frac{1}{x}\,dx = ln\,|x|\,+ C\]Furthermore, we can use the multiplier constant rule to establish that:
\[\int \frac{a}{x}\,dx = a\,ln\,|x|\,+ C\]Example 1:
Find the antiderivative of \(f(x) = \frac{2}{x}\)
Solution:
\[\int \frac{2}{x}\,dx = 2\,ln\,|x|\,+ C\]Example 2:
Calculate the integral below. Give your answer to two decimal places.
\[\int_1^2 \frac{1}{4x}\,dx\]Solution:
\[\begin{aligned} \int_1^2 \frac{1}{4x}\,dx &= \frac{ln\,(2)}{4} - \frac{ln\,(1)}{4} \\\ &= \frac{ln\,(2)}{4} - 0 \\\ &= \frac{ln\,(2)}{4} \\\ &= 0.17 \\\ \end{aligned}\]Sum and difference
To find the integral of two (or more) functions that are being added together or subtracted from each other, we can find the integral of each one separately first, and keep the relevant operation.
The integral of \(y\,=\,f(x)\,\pm\,g(x)\) will be:
\[\int (f(x)\,\pm\,g(x))\,dx = \int f(x)\,dx \pm \int g(x)\,dx\]Example 1:
Find the antiderivative:
\[\int (sin\,x - 3x^2 + 7x - 4)\,dx\]Solution:
\[\begin{aligned} \int (sin\,x - 3x^2 + 7x - 4)\,dx &= \int sin\,x\,dx - \int 3x^2\,dx + \int 7x\,dx - \int 4\,dx \\\ &= -cos\,x - \frac{3x^3}{3} + \frac{7x^2}{2} - 4x + C \\\ \end{aligned}\]Example 2:
Evaluate the definite integral below. Give your answer to 3 decimal places.
\[\int_5^{10} (3x - cos\,x)\,dx\]Solution:
\[\begin{aligned} \int_5^{10} (3x - cos\,x)\,dx &= \int_5^{10} 3x\,dx - \int_5^{10} cos\,x\,dx \\\ &= (\frac{3(10^2)}{2} - \frac{3(5^2)}{2}) - (sin\,10 - sin\,5) \\\ &= (150 - 37.5) - ((-0.544) - (-0.959)) \\\ &= 112.5 - 0.415 \\\ &= 112.085 \end{aligned}\]Check your understanding of the rules of integration by working through the questions below:
Integration by substitution
In some specific cases, we can use integration by substitution to find the integral of a function. This method is also known as \(u\)-substitution as it involves using the letter \(u\) to represent part of the function we are integrating, or as the reverse chain rule as it requires you to recognise the derivative of a function.
Given two functions \(f(x)\) and \(g(x)\), we can use integration by substitution if our integral looks like this:
\[\int f(g(x))\;g'(x)\,dx\]Leaving the above as it is would make finding the integral difficult, but we can change it to make it simpler for ourselves using integration by substitution. Specifically, we let \(u = g(x),\) which gives \(g'(x)\,dx = (\frac{du}{dx})\,dx = du.\) The integral is then simplified as shown below.
Integration by substitution says that if we have:
\[\int f(g(x))\;g'(x)\,dx\]then we can substitute \(u = g(x)\) and \(du = g'(x)\,dx\) to give:
\[\int f(u)\,du\]We can then integrate with respect to \(u,\) before substituting \(g(x)\) back into the answer to remove \(u.\) Note also that even if the integral is not in the stated format, you can still integrate by substitution by taking out a multiplier constant as required.
Example 1:
Evaluate \(\int ln(2x+3)\,dx\)
Solution:
For this example it makes sense to use \(u = 2x+3.\) However, the derivative of \(2x+3\) is \(2\) and we don’t have this in our integral. We can fix this by including it in the integral as \(g'(x)\) and then taking out the multiplier constant of \(\frac{1}{2}\) to compensate though, as follows:
\[\int ln(2x+3)\,dx = \frac{1}{2}\int 2\,ln(2x+3)\,dx\]We can then use integration by substitution with \(u = 2x+3\) to give:
\[\begin{aligned} \frac{1}{2}\int 2\,ln(2x+3)\,dx &= \frac{1}{2}\int ln\,u\,du \\\ &= \frac{1}{2}\,u(ln\,u - 1) + C \\\ \end{aligned}\]Finally, we can substitute \(u = 2x + 3\) back into this answer to remove the variable \(u\) and therefore evaluate the original integral:
\[\int ln(2x+3)\,dx = \frac{2x+3}{2}\,(ln (2x+3) - 1) + C\]Example 2:
Calculate the definite integral of \(f(x) = 2x(1+x^2)^3\) from \(x=0\) to \(x=1\)
Solution:
Looking at our integral, \(\int_0^1 2x(1+x^2)^3\,dx\) we can see that \(2x\) is the derivative of \(1 + x^2\), and therefore we can use \(u = 1 + x^2\)
While we don’t need to make any changes to what is being integrated in this example, because we are changing the variables in the integral we do need to change the limits of the integral so that they are related to the new variable \(u\). We do this by finding the value of \(u\) at the given limits, which in this example is at \(x=0\) and \(x=1\)
So, at \(x=0\):
\[\begin{aligned} u &= 1+(0)^2 \\\ &= 1 \\\ \end{aligned}\]And, at \(x=1\):
\[\begin{aligned} u &= 1+(1)^2 \\\ &= 2 \\\ \end{aligned}\]Therefore our integral, after substitution, is now:
\[\int_1^2\,u^3\, du\]Now we can calculate the definite integral:
\[\begin{aligned} \int_1^2\,u^3\, du &= \frac{(2)^4}{4} - \frac{(1)^4}{4} \\\ &= \frac{16}{4} - \frac{1}{4} \\\ &= \frac{15}{4} \\\ \end{aligned}\]Check your understanding of integration by substitution by working through the questions below:
If we let \(u = x^2,\) this has the derivative \(2x\) and hence the integral is in the required form to use integration by substitution as follows:
\[\begin{aligned} \int 2xe^{x^2}\,dx &= \int e^u du \\\ &= e^u + C \\\ &= e^{x^2} + C \\\ \end{aligned}\]If we let \(u = x^2 + 1,\) this has the derivative \(2x\) and hence the integral is in the required form to use integration by substitution. However, we do need to change the limits from \(x=0\) to \(u=1\) and from \(x=1\) to \(u=2.\) We can then evaluate the integral as follows:
\[\begin{aligned} \int_0^1 \frac{2x}{(x^2 + 1)^2}\,dx &= \int_1^2 \frac{1}{u^2}\,du \\\ &= \int_1^2 u^{(-2)}\,du \\\ &= [\frac{u^{-1}}{-1}]_1^2 \\\ &= [-\frac{1}{u}]_1^2 \\\ &= -(\frac{1}{2} - \frac{1}{1}) \\\ &= - \frac{1}{2} + 1 \\\ &= \frac{1}{2} \end{aligned}\]We can use \(u = 1 + cos\,x,\) however since this has the derivative \(-sin\,x\) we need to rewrite the integral as:
\[-\int_0^{\frac{\pi}{2}} \frac{-sin\,x}{1 + cos\,x} dx\]We also need to rewrite the defined limits in terms of \(u\):
\[\begin{aligned} u &= 1 + cos\,0 \\\ &= 2 \end{aligned}\] \[\begin{aligned} u &= 1 + cos\,\frac{\pi}{2} \\\ &= 1 \end{aligned}\]Therefore, the integral can be evaluated as follows:
\[\begin{aligned} \int_0^{\frac{\pi}{2}} \frac{sin\,x}{1 + cos\,x} dx &= -\int_0^{\frac{\pi}{2}} \frac{-sin\,x}{1 + cos\,x}\,dx \\\ &= - \int_2^1 \frac{1}{u}\,du \\\ &= \int_1^2 \frac{1}{u}\,du \\\ &= ln\,2 - ln 1 \\\ &= ln\,2 \\\ \end{aligned}\]Integration by parts
When we have the product of two functions, we can use integration by parts to find the integral. In order to understand how integration by parts works, we need to think back to derivatives and specifically to the product rule. This says that if we have:
\[y\,=\,f(x)\,\times\,g(x)\]then the derivative will be:
\[\frac{dy}{dx}\,=\,g(x)\,\times\,f'(x)\;+\;f(x)\,\times\,g'(x)\]If we rewrite the above formula using integration notation, we know that this must also be true:
\[f(x)\,\times\,g(x) = \int\,(g(x)\,\times\,f'(x)\;+\;f(x)\,\times\,g'(x))\,dx\]This can also be written as:
\[f(x)\,\times\,g(x) = \int\,g(x)\,\times\,f'(x)\, dx + \int\,f(x)\,\times\,g'(x)\,dx\]When we rearrange this we get the formula for integration by parts:
\[\int\,f(x)\,\times\,g'(x)\,dx = f(x)\,\times\,g(x) - \int\,g(x)\,\times\,f'(x)\, dx\]where \(f(x)\) and \(g(x)\) are two functions, \(f'(x)\) is the derivative of \(f(x)\) and \(g'(x)\) is the derivative of \(g(x)\)
Example 1:
Find \(\int\,x\,sin\,x\,dx\)
Solution:
To evaluate this we need:
\[\int\,x\,sin\,x\,dx = \int\,f(x)\,\times\,g'(x)\,dx\]So let \(f(x) = x\) and \(g'(x) = sin\,x,\) which means \(f'(x) = 1\) and \(g(x) = -\,cos\,x.\) Our indefinite integral can then be evaluated in parts as follows:
\[\begin{aligned} \int\,x\,sin\,x\,dx &= x(-cos\,x) - \int(-cos\,x)\,dx \\\ &= -x\,cos\,x + \int cos\,x\,dx \\\ &= -x\,cos\,x + sin\,x + C \\\ \end{aligned}\]Example 2:
Evaluate \(\int_0^{\pi} x^2\,cos\,x\,dx\)
Solution:
Let \(f(x) = x^2\) and \(g'(x) = cos\,x,\) which means \(f'(x) = 2x\) and \(g(x) = sin\,x.\) Our definite integral can then be rewritten as follows:
\[\int_0^{\pi}\,x^2\,cos\,x\,dx = [x^2\,sin\,x]_0^{\pi} - \int_0^{\pi}\,2x\,sin\,x\,dx\]Note that since we don’t need to find the integral of \(x^2\,sin\,x\), we use square brackets with the limits to denote that we still need calculate this part of the formula at those values of \(x\). Doing this gives:
\[\begin{aligned} \,[x^2\,sin\,x]_0^{\pi} &= {\pi}^2 \times sin(\pi) - 0^2 \times sin\,(0) \\\ &= 0 \\\ \end{aligned}\]Next we need to integrate the second half of our formula \(\int_0^{\pi}\,2x\,sin\,x\,dx,\) which we can do using integration by parts again. This time let \(f(x) = 2x\) and \(g'(x) = sin\,x,\) so \(f'(x) = 2\) and \(g(x) = - cos\,x\) and we have:
\[\begin{aligned} \int_0^{\pi}\,2x\,sin\,x\,dx &= [-2x\,cos\,x]_0^{\pi} - \int_0^{\pi} -2\,cos\,x\,dx \\\ &= -[2x\,cos\,x]_0^{\pi} + 2\,\int_0^{\pi}\,cos\,x\, dx \\\ \end{aligned}\]Now we calculate \(-[2x\,cos\,x]_0^{\pi}\) as follows:
\[\begin{aligned} -[2x\,cos\,x]_0^{\pi} &= -2(\pi)\,cos\,(\pi) - -2(0)\,cos\,(0) \\\ &= 2 \pi \\\ \end{aligned}\]Next we calculate the second half of this integral:
\[\begin{aligned} 2 \int_0^{\pi}\,cos\,x\,dx &= 2(sin\,(\pi) - sin\,(0)) \\\ &= 0 \\\ \end{aligned}\]Therefore we have established that the second half of our original integral is:
\[\begin{aligned} \int_0^{\pi}\,2x\,sin\,x\,dx &= 2 \pi + 0 \\\ &= 2 \pi \\\ \end{aligned}\]Finally, we can use all of this to calculate the answer to our original integral:
\[\begin{aligned} \int_0^{\pi} x^2\,cos\,x\,dx &= [x^2\,sin\,x]_0^{\pi} - \int_0^{\pi}\,2x\,sin\,x\,dx \\\ &= 0 - 2 \pi \\\ &= -2 \pi \\\ \end{aligned}\]Check your understanding of integration by parts by working through the questions below:
Let \(f(x) = x\) and \(g'(x) = e^{2x},\) which means \(f'(x) = 1\) and \(g(x) = \frac{e^{2x}}{2}\)
So using our integration by parts formula, we have:
\[\begin{aligned} \int xe^{2x}\,dx &= \frac{xe^{2x}}{2} - \int \frac{e^{2x}}{2} \\\ &= \frac{xe^{2x}}{2} - \frac{e^{2x}}{4} + C \\\ &= \frac{e^{2x}}{4} (2x - 1) + C \\\ \end{aligned}\]Let \(f(x) = x\) and \(g'(x) = e^x,\) which means \(f'(x) = 1\) and \(g(x) = e^x\)
So using our integration by parts formula, we have:
\[\begin{aligned} \int_0^1 xe^x\,dx &= [xe^x]_0^1 - \int_0^1 e^x\,dx \\\ &= (1e^1 - 0 \times e^0) - (e^1 - e^0) \\\ &= e - (e - 1) \\\ &= 1 \end{aligned}\]Let \(f(x) = ln\,x\) and \(g'(x) = x^2,\) which means \(f'(x) = \frac{1}{x}\) and \(g(x) = \frac{x^3}{3}\)
So using our integration by parts formula, we have:
\[\begin{aligned} \int x^2\,ln\,x\,dx &= \frac{x^3\,ln\,x}{3} - \int \frac{x^2}{3} \\\ &= \frac{x^3\,ln\,x}{3} - \frac{x^3}{9} + C\\\ \end{aligned}\]