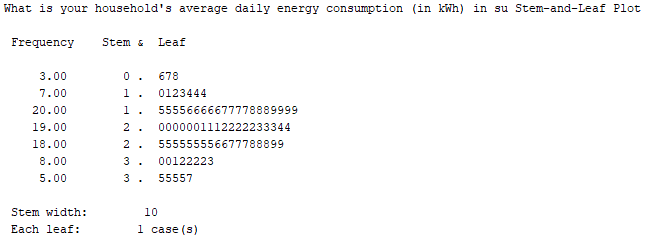Introduction to SPSS
Many of the statistics detailed in the Inferential statistics page of this module rely on the assumption that continuous data approximates a normal distribution, or that the sample size is large enough that the sampling distribution of the mean approximates a normal distribution. This page details how to use SPSS to test whether a continuous variable is normally distributed, while the Introduction to statistics module provides more information about what the normal distribution is and when testing for it is required.
The examples covered make use of the Household energy consumption data.sav file, which contains fictitious data for 80 people based on a short ‘Household energy consumption’ questionnaire. If you want to work through the examples provided you can download the data file using the following link:
If you would like to read the sample questionnaire for which the data relates, you can do so using this link:
Before commencing the analysis, note that the default is for dialog boxes in SPSS to display any variable labels, rather than variable names. You may find this helpful, but if you would prefer to view the variable names instead then from the menu choose:
- Edit
- Options…
- Change the Variable Lists option to Display names
Testing for normality
As explained in the Introduction to statistics module, it is helpful to consult a number of different measures in order to make a decision about normality. The Explore procedure in SPSS allows you to do this.
For example, to test whether the ‘q6’ variable (which measures average daily summer energy consumption in kWh in the sample data file) is normally distributed, choose the following from the SPSS menu (either from the Data Editor or Output window):
- Analyze
- Descriptive Statistics
- Explore…
- move the variable that you are checking for normality (in this case ‘q6’) into the Dependent List
- click on the Plots… button
- tick the Histogram box (keep the Stem-and-leaf box ticked as well)
- tick the Normality plots with tests option
- click on Continue
- click on OK
The output should be as follows:

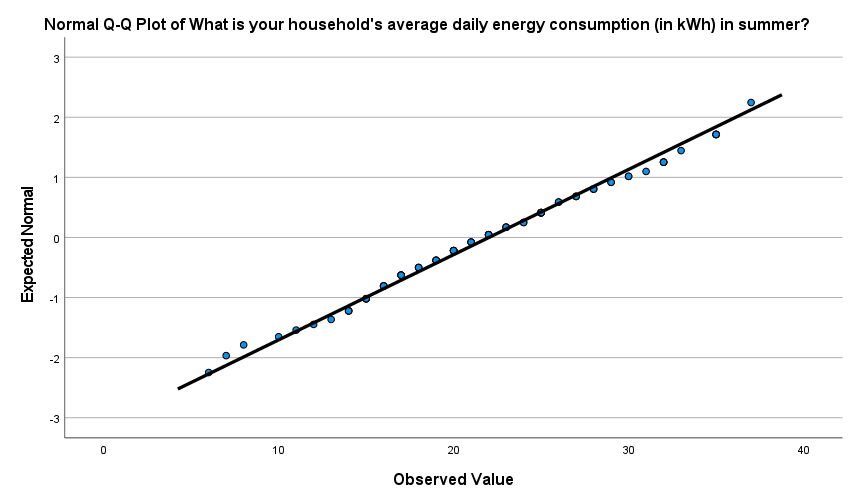
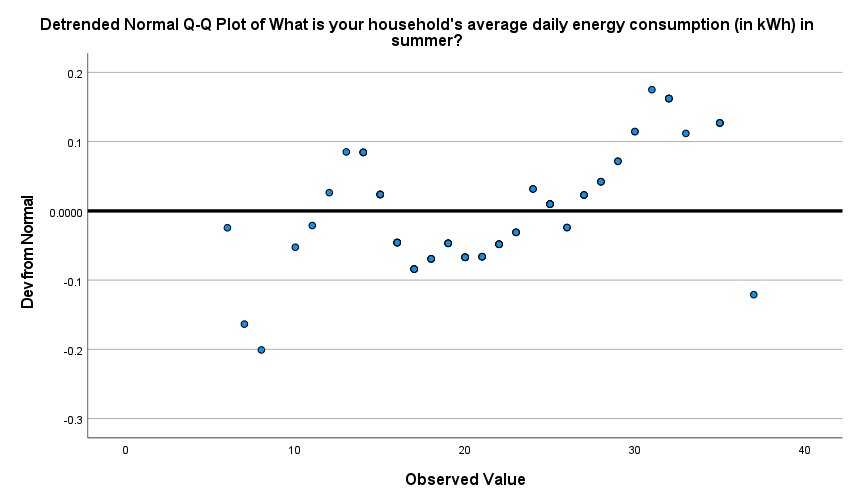
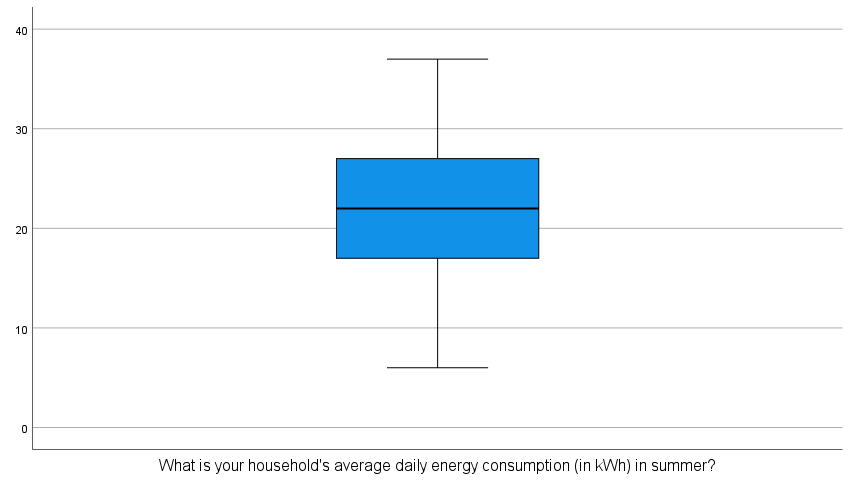
This output can then be evaluated as explained in the Introduction to statistics module. In particular, you should observe the following:
-
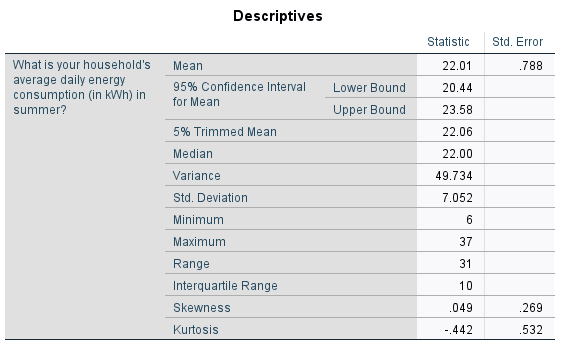
The mean and median (as shown in the ‘Descriptives’ table) are extremely similar. Note that if you would also like to compare the mode, you can obtain this through the Frequencies procedure as described in the Descriptives statistics page of this module. While this is a bit higher, at \(25\), this is less of a concern.
-
The skewness is \(0.049\) (as shown in the ‘Descriptives’ table), which is well within the acceptable range of \(-1\) to \(1\)
If you want you can also calculate the z-score by dividing this by the skewness standard error of \(0.269\) (also shown in the ‘Descriptives’ table), to give \(0.182\)
This is well within the acceptable range of \(-1.96\) to \(1.96\) -
The kurtosis is \(-0.442\) (as shown in the ‘Descriptives’ table), which is within the acceptable range of \(-1\) to \(1\)
If you want you can also calculate the z-score by dividing this by the kurtosis standard error of \(0.532\) (also shown in the ‘Descriptives’ table), to give \(0.831\)
This is within the acceptable range of \(-1.96\) to \(1.96\) -
The \(p\) value for the Shapiro-Wilk test is \(.585\) (as listed under ‘Sig.’ in the ‘Tests of Normality’ table), which is greater than \(.05\) as required.
-
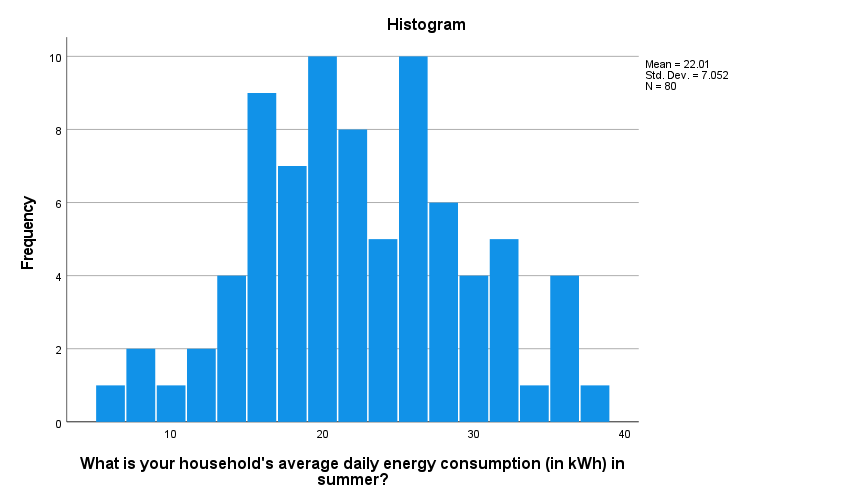
The histogram is roughly symmetrical. Note that you can double click on the graph in SPSS to open the Chart Editor , then select the Elements drop down menu and choose Show Distribution Curve , to add in the normal curve in order to assess symmetry if desired.
-
The stem and leaf plot is roughly symmetrical.
-
The points do not deviate much from the line in the Normal Q-Q plot, and there are roughly equal number of points above and below the line in the detrended Q-Q plot.
-
The median is approximately in the middle of the box plot, the whiskers are of similar length and there are no outliers.
Hence it can be concluded that the ‘q6’ variable is approximately normally distributed.
Transforming variables
If you find that a variable is not normally distributed when you require it to be, you can try transforming the variable to see if this makes it better approximate a normal distribution. Some examples of transformations to try are provided in the Introduction to statistics module.
You can apply any of these transformations to the variable using the Compute variable procedure, as described in the Transformations page of this module. Once you have done this, you will need to test again for normality in the usual way.
Testing for normality in two or more groups
Sometimes rather than testing that all of a continuous variable’s data is normally distributed, you need to check that the continuous variable’s data is normally distributed for each category of a categorical variable. Again, you can do this using the Explore procedure.
For example, to test whether the ‘q6’ variable (which measures average daily summer energy consumption in kWh in the sample data file) is normally distributed for both groups of the ‘q3’ variable (which shows whether or not the participant has any children in the sample data file), choose the following from the SPSS menu (either from the Data Editor or Output window):
- Analyze
- Descriptive Statistics
- Explore…
- move the variable that you are checking for normality (in this case ‘q6’) into the Dependent List
- move the grouping variable (in this case ‘q3’) into the Factor List
- click on the Plots… button
- tick the Histogram box (keep the Stem-and-leaf box ticked as well)
- tick the Normality plots with tests option
- click on Continue
- click on OK
The output will be very similar to the output obtained when no factor is added, but this time there will be a set of statistics and graphs for each group. These should be analysed separately, and you may sometimes find that the data is normally distributed for all groups, for some groups only, or for none of the groups. In this case, the output indicates that the ‘q6’ variable is normally distributed for both the group that has children, and the group that doesn’t.