Numeracy fundamentals
This page takes you through some important concepts on the topics of measurement and geometry, with activities to consolidate your knowledge along the way. For more sample questions on these concepts, in particular if you are preparing for the Literacy and Numeracy Test for Initial Teacher Education (LANTITE), you may like to visit the LANTITE page. Alternatively, if you would like to build up some more advanced skills on the topic of geometry, you may like to visit the Geometry and trigonometry module.
As you work through the content keep in mind that there are often different ways of solving the same problem. While in some cases alternative methods have been explained, for many examples just one method of working is provided. If you already know a different technique for solving the problem then that’s great (provided it is also correct, of course). Don’t feel you need to change your method - the important thing is that you use a technique that makes sense to you.
In brief, this page covers how to do the following:
- Convert units of measurement
- Draw diagrams to help solve problems involving measurement
- Solve problems involving time
- Use distance and time to calculate speed
- Interpret directions
- Calculate perimeter, area and volume of simple shapes
Converting between units
The metric system of measurement is an international system of units of measurement which is based on the decimal (or base \(10\)) number system. The system uses two kinds of units; base units and derived units. The base unit of measurement for three common types of measurement are as follows:
| Measurement | Unit | Abbreviation |
|---|---|---|
| Length | metre | m |
| Volume | litre | L |
| Weight | gram | g |
From these base units of measurement, other units of measurement are derived to show smaller or larger multiples of the base unit. This is done by way of an appropriate prefix which is added to the base unit to indicate how it has been altered. The most commonly used are:
| Metric prefix | Relation to base unit | Abbreviation | Derived units |
|---|---|---|---|
| kilo | 1000 times bigger | k | kilometre (km), kilolitre (kL), kilogram (kg) |
| centi | 100 times smaller | c | centimetre (cm) |
| milli | 1000 times smaller | m | millimetre (mm), millilitre (mL), milligram (mg) |
When solving a problem involving measurements, you need to ensure that all measurements of the same type are in the same unit. If they aren’t, you can convert from one unit to another by making use of the relationships detailed in the table above.
Example: Suppose you wish to tile the floor of a room that is \(3\textrm{m}\) wide with small tiles of width \(50\textrm{mm}\). How many tiles will you need to cover the width of the room?
Solution: To solve this you first need both measurements to be in the same unit. If you wish to have them both in metres, for example, you could convert the measurement that is in millimetres to metres by dividing by \(1000\):
\(50\textrm{mm} \div 1000 = 0.05\textrm{m}\)
Alternatively, if you wish to have them both in millimetres you could convert the measurement that is in metres by multiplying it by \(1000\):
\(3\textrm{m} \times 1000 = 3000\textrm{mm}\)
Once the measurements are both in the same unit, you can simply divide one by the other:
Method 1: \(3\textrm{m} \div 0.05\textrm{m} = 60\)
Method 2: \(3000\textrm{mm} \div 50\textrm{mm} = 60\)
Either way, \(60\) tiles are required.
Some other common equivalent measurements you may need to convert between are:
- \(1\textrm{cm} = 10\textrm{mm}\)
- \(1\textrm{ metric tonne} = 1000\textrm{kg}\)
- \(1\textrm{ hectare} = 10000\textrm{m}^2\)
- \(1\textrm{ hectare} \approx 2.471\textrm{ acres}\) (an imperial measurement)
If you ever forget whether to divide or multiply when converting, just think about the relative size of the different units and whether the conversion makes sense (millimetres are much smaller than metres, for example, so you need a lot of them to make a small amount of metres). You can also use your knowledge of rates and proportion to ensure the conversion is correct (refer to the Ratios, rates and proportions section if required).
Example: Suppose you are considering purchasing a property that is listed as being \(5\) acres. How big is the property in hectares?
Solution: If you wish to convert this to the metric unit of hectares, you have the following complete and incomplete rates:
\[\begin{aligned} 1 \textrm{ hectare} &= 2.471 \textrm{ acres} \\\ ? \textrm{ hectares} &= 5 \textrm{ acres} \end{aligned}\]Therefore, since \(5 \div 2.471 \approx 2.023\), it follows that \(5\textrm{ acres}\) is equivalent to \(2.023\textrm{ hectares}\).
Once you have worked through the examples above, have a go at the conversion problems in the following activity:
Drawing diagrams
Never underestimate the power of a simple diagram to assist you with solving a measurement problem, as they can be really helpful.
Example: Suppose you have a piece of cardboard measuring \(1.4\textrm{m}\) by \(1.2\textrm{m}\) and you want to cut it into squares of size \(25\textrm{cm} \times 25\textrm{cm}\) for a craft activity. You need \(23\) squares - will you be able to cut enough, or will you require some extra cardboard?
Solution: The first thing to do here is to convert the measurements to have them all in the same unit. Having all lengths in metres only requires one conversion, so doing this gives:
\(25\textrm{cm} \div 100 = 0.25\textrm{m}\)
Next, you might be tempted to find the area of the card and divide it by the area of the pieces you want to cut - but this doesn’t take into account the fact that you might have some unused strips of paper at the sides. A diagram illustrates this, and shows that instead you need to treat the length and width separately:
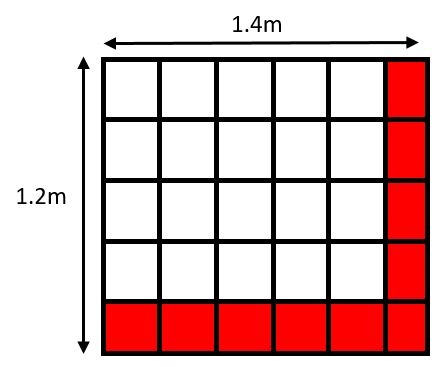
Doing this gives:
\(1.4 \div 0.25 = 5.6\), meaning \(5\) pieces can be cut from the length
\(1.2 \div 0.25 = 4.8\), meaning \(4\) pieces can be cut from the width
(Note you need to truncate - cut off - rather than round in both instances.)
Therefore \(5 \times 4 = 20\) pieces can be cut altogether, so you will need some extra cardboard.
Once you have worked through the example above, have a go at using diagrams to solve the problems in the following activity:
Time
Another concept you may need to work with measurements for is time. Some common calculations you might need to perform involving time include finding the duration of events and determining differences between times. There are a couple of different ways of doing this.
Example: Suppose you are timing a race, and the times for the first three competitors in minutes and seconds are \(23\):\(56\), \(24\):\(01\) and \(25\):\(12\). How much slower was the third placed competitor compared to the first?
Solution: There are a few different methods to find out the difference in minutes and seconds between \(23\):\(56\) (first) and \(25\):\(12\) (third).
For example, one approach is to convert both times to seconds by multiplying the minutes by 60 and adding the existing seconds, as follows:
\(23 \times 60 + 56 = 1436\textrm{ seconds}\), and \(25 \times 60 + 12 = 1512\textrm{ seconds}\)
You can then calculate the difference in seconds, which is:
\(1512 – 1436 = 76 \textrm{ seconds}\)
Finally, you can convert this difference back to minutes and seconds by dividing through by \(60\). When you do this the whole number part gives the number of minutes, while the decimal part can be multiplied by \(60\) again to give the number of seconds, as follows (note that the dot over the \(6\) indicates that the decimal is recurring - meaning it repeats forever):
\(76 \div 60 = 1.2\dot{6}\), and \(0.2\dot{6} \times 60 = 16\)
So the answer is \(1 \textrm{ minute}\) and \(16 \textrm{ seconds}\).
Another approach is to work it out in stages. For example, first of all you could calculate how many seconds are between \(23\):\(56\) and \(24\):\(00\), by subtracting \(56\) from \(60\) (i.e. \(60 – 56 = 4 \textrm{ seconds}\)). Then you could work out how many minutes are between \(24\):\(00\) and \(25\):\(00\) (i.e. \(25 – 24 = 1 \textrm{ minute}\)), and finally you could add on the extra \(12 \textrm{ seconds}\) from \(25\):\(12\) to give \(4 + 12 = 16 \textrm{ seconds}\).
So again the answer is \(1 \textrm{ minute}\) and \(16 \textrm{ seconds}\).
Once you have worked through the example above, have a go at the time problems in the following activity:
Speed
Once you are familiar with distance and time, you can use them to calculate the rate at which a distance is being travelled; otherwise known as speed. You can do this using the following formula:
\[\textrm{speed} = \frac{\textrm{distance}}{\textrm{time}}\]Example: Suppose you have just started a new job that is \(18\textrm{km}\) from your house, and you plan to ride your bike there. If you need to be at work at \(8\textrm{am}\) and you plan to leave your house at \(7.15\textrm{am}\), what will be the average speed you need to ride in kilometres per hour?
Solution: To calculate this, first note that you need to work out how much time you have in hours. Since you leave at \(7.15\textrm{am}\) and need to arrive by \(8\textrm{am}\) this gives a total time of \(45 \textrm{ minutes}\), and \(45 \div 60 = 0.75 \textrm{ hours}\).
Therefore your average speed will need to be: \(\frac{18}{0.75} = 24 \textrm{ km/hr}\)
Alternatively, \(\frac{18}{45} = 0.4 \textrm{ km/min}\) and \(0.4 \times 60 = 24 \textrm{ km/hr}\)
Once you have worked through the example above, have a go at the speed problem in the following activity:
Directions
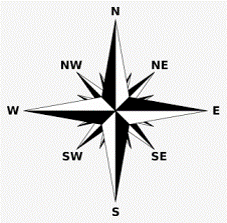
Being able to read maps and interpret directions is an important skill. The two types of directions you may need to interpret are the four cardinal directions (north, east, south and west), and left and right directions.
When interpreting cardinal directions on a map, there is often an arrow indicating which way is north (in the absence of this, it is safe to assume that north is at the top of the map). Once you know which way is north, there are different mnemonics you can use to remember the rest of the directions. For example, the letters in N ever E at S oggy W eetbix indicate that the clockwise order of the directions are N orth E ast S outh W est.
There are also intermediate directions located halfway between these directions, as illustrated:
In terms of left and right, it can be helpful to try and imagine yourself orientated in the direction you are ‘travelling’ on the map (or actually reorient yourself or turn the map if possible!), as left and right will vary accordingly. And if you forget left and right, just hold both hands up in front of you and try to make an ‘L’ shape with your fingers and thumb- the one that looks correct is your left hand.
Example: Suppose you are travelling south down Conway St and turn left on Allen St on the map shown. Will you make it to the shopping centre?
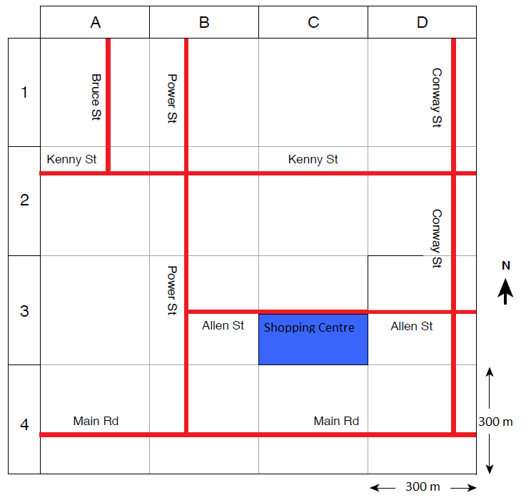
Solution: To figure this out, first note that north is at the top of the map, which means that south is at the bottom and that if you are travelling south down Conway St you are travelling ‘down’ the map. So try to imagine that when you get to Allen St you are coming at it from the ‘top’ side, facing downwards, and therefore that if you go left, you would go off the map and not towards the shopping centre.
Alternatively, you might like to try and remember that if you are travelling ‘down’ the map, the directions will be the opposite of what they would be if you were travelling ‘up’. So while it looks like the shopping centre is to the left of Conway St, actually you would need to turn right.
Once you have worked through the example above, have a go at the direction problems in the following activity:
Perimeter
The perimeter of a shape is the distance around the outside. For example, the perimeter of a rectangle is just the sum of the \(4\) sides, which equates to \(2\) times the length plus \(2\) times the width. \(\textrm{Perimeter of rectangle} = 2 \times \textrm{length} + 2 \times \textrm{width}\)

You may also need to find the perimeter of irregular shapes. Sometimes this might require adding up the lengths of all the different sides, while at other times there may be a shortcut way of calculating the perimeter based on the perimeter of the shape or shapes the irregular shape is adapted from.
Example: What is the perimeter of the following shape?

Solution: One way of calculating the perimeter of this shape is to start by calculating the total perimeter of both the squares, which is \(12\textrm{cm} \times 4 + 12\textrm{cm} \times 4 = 96\textrm{cm}\)
Next, since both squares have been pushed together, there is a small part of the perimeter of each square that needs to be subtracted from this total. From the \(9\textrm{cm}\) distance on the diagram, we can work out that the distance that needs to be subtracted is two lots of \(3\textrm{cm}\) (since \(12\textrm{cm} - 9\textrm{cm} = 3\textrm{cm}\))
Therefore the perimeter of the irregular shape is \(96\textrm{cm} - 3\textrm{cm} - 3\textrm{cm} = 90\textrm{cm}\)
Once you have worked through the example above, have a go at the perimeter problems in the following activity:
Area
The area of a shape is the space inside the boundary. The most common area you will likely be required to work out is that of a rectangle, which simply requires multiplying the length by the width: \(\textrm{Area of rectangle} = \textrm{length} \times \textrm{width}\)

If you need to calculate the area of a triangle, this is simply half the base times the height: \(\textrm{Area of triangle} = \frac{1}{2} \times \textrm{base} \times \textrm{height}\)

Example: What is the area of the following triangle?
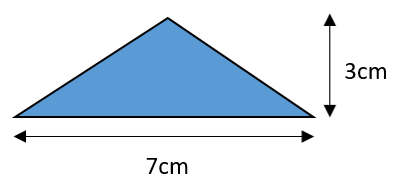
Solution: The area of this triangle is \(\frac{1}{2} \times 7\textrm{cm} \times 3\textrm{cm} = 10.5\textrm{cm}^2\)
Once you have worked through the example above, have a go at the area problems in the following activity:
Volume
The volume of a shape is the amount of 3D space inside it. Volume can be measured in cubic metres (or cubic centimetres, cubic millimetres, etc.), or it can be measured in litres (or millilitres, kilolitres, etc.). The relationship between these two kinds of measurements is as follows:
\(1 \textrm{litre} = 1000\textrm{cm}^3\)
Example: Suppose you have a rectangular fish tank that measures \(50\textrm{cm}\) long by \(30\textrm{cm}\) wide and \(40\textrm{cm}\) high. If you want to fill it three quarters of the way up, what would be the volume of water required in litres?
Solution: To do this you would first calculate the volume by multiplying the three measurements:
\(50\textrm{cm} \times 30\textrm{cm} \times 40\textrm{cm} = 60000\textrm{cm}^3\)
Next, three quarters of this volume is:
\(60000\textrm{cm}^3 \times \frac{3}{4} = 45000\textrm{cm}^3\)
Finally, you can convert to litres by dividing through by \(1000\):
\(45000\textrm{cm}^3 \div 1000 = 45 \textrm{ litres}\) required
Once you have worked through the example above, have a go at the volume problem in the following activity: