Introduction to algebra
This page explains some techniques for solving quadratic equations. In particular, the page covers the following (use the drop-down menu above to jump to a different section as required):
- What is a quadratic equation?
- Solving when \(b = 0\)
- Solving by factorising
- Solving using the quadratic formula
What is a quadratic equation?
A quadratic equation, or second degree equation, is an algebraic equation of the form:
\[ax^2 + bx + c = 0,\]where \(x\) is a variable and \(a\), \(b\) and \(c\) represent known numbers such that \(a \neq 0\) (if \(a = 0\) then the equation is linear). These are referred to as coefficients of the equation.
The most basic quadratic equation occurs when \(a = 1\), \(b = 0\) and \(c = 0\), in which case we have:
\[x^2 = 0\]In this case you should be able to see that the value of the variable \(x\) must be \(0\), as only \(0^2 = 0\). So the solution to this quadratic equation is \(0\).
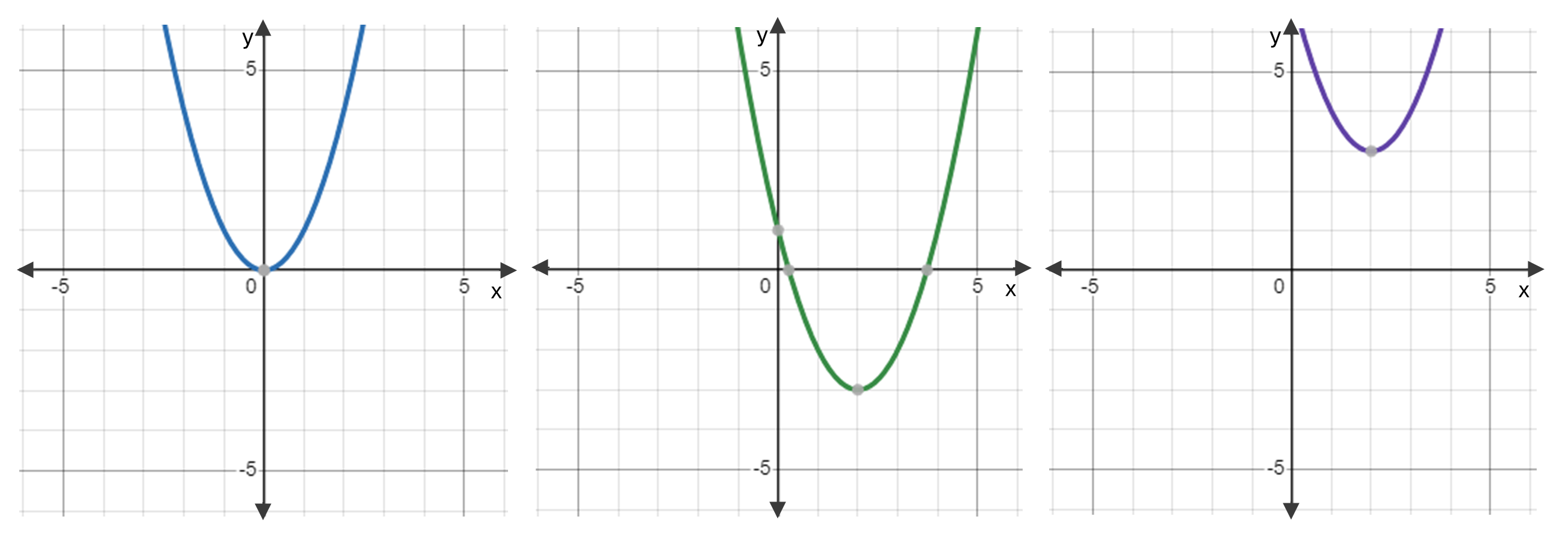
While this quadratic equation has only one solution, note that often there will be two solutions, and sometimes there will be no (real) solutions at all. To understand why this is the case, it can be helpful to look at the graphs of some quadratic equations. As seen below these take the form of parabolas, and the places at which these parabolas intersect the \(x\) (horizontal) axis are the solutions to the equation (as this is when the equation is equal to \(0\)).
The first image below is an example of where the parabola only intersects the \(x\) axis once, and hence there is only one solution (this is actually a plot of \(y = x^2\), although no scales are included on the axes). The second image is an example of where the parabola intersects the \(x\) axis twice, and hence there are two solutions, and finally the third image is an example of where the parabola does not intersect the \(x\) axis at all - and hence there are no solutions.
There are various ways of solving quadratic equations, depending on the nature of the equation. This page outlines three different techniques.
Solving when \(b = 0\)
Probably the easiest type of quadratic equation to solve is one where \(b = 0\); i.e. when the equation is of the form:
\[ax^2 + c = 0\]You can solve equations like this as follows:
-
Rearrange the equation so that \(ax^2\) is by itself on the left hand side of the equation, by adding or subtracting the constant \(c\) from both sides, as applicable; like you would do for a linear equation.
-
Divide through both sides of the equation by \(a\) (assuming \(a \neq 1\)); like you would do for a linear equation.
- Take the square root of both sides of the equation, keeping in mind that this may result in either:
- no real solution, if you are taking the square root of a negative number (as there is no real number that can be squared to make a positive number);
- one solution of \(0\), if you are taking the square root of \(0\); or
- both a positive and a negative solution, if you are taking the square root of a positive number. For example, \(\sqrt{100} = \pm 10\) (“plus or minus ten”), as both \(10\) and \(-10\) are square roots of \(100\).
- Check that the answer(s) you have obtained is/are actually correct, by substituting the value back into the original equation and evaluating it. If it’s not correct, go back and see if you can find where you went wrong and work through the steps again.
Example: Solve the quadratic equation \(2x^2 - 72 = 0\)
Solution: Following the steps above, we have:
\[\begin{aligned} && 2x^2 - 72 &= 0 && \\\ \therefore && 2x^2 - 72 + 72 &= 0 + 72 && \textrm{ (undo subtraction by adding) } \\\ \therefore && 2x^2 &= 72 && \textrm{ (simplify) } \\\ \therefore && \frac{2x^2}{2} &= \frac{72}{2} && \textrm{ (divide both sides by 2) } \\\ \therefore && x^2 &= 36 && \textrm{ (simplify) } \\\ \therefore && \sqrt{x^2} &= \sqrt{36} && \textrm{ (take square root of both sides) } \\\ \therefore && x &= \pm 6 && \textrm{ (evaluate - equation is solved!) } \end{aligned}\]Finally, substituting \(\pm 6\) back into the original equation gives \(2(\pm 6)^2 - 72 = 2(36) - 72 = 72 - 72 = 0\) as required. So the solution is correct.
Once you have worked through the example above, have a go at using this technique to find the value of \(x\) in some or all of the following quadratic equations:
Solving by factorising
Another way you can solve a quadratic equation is by factorising the equation using two sets of brackets. This isn’t always easy or even possible, but if you notice that the equation can be relatively easily factorised, this can be a quick method of solving it. You can solve like this as follows:
-
Factorise the quadratic equation, as detailed in the Factorising section of this module.
-
In order for the quadratic equation to equal zero at least one of the factors must be zero, so you can solve it by setting each factor equal to zero and solving - like you would for a linear equation.
-
Check that the answer(s) you have obtained is/are actually correct, by substituting the value back into the original equation and evaluating it. If it’s not correct, go back and see if you can find where you went wrong and work through the steps again.
Example: Solve the quadratic equation \(x^2 + 7x + 12 = 0\)
Solution: Following the steps above, we have:
-
\(x^2 + 7x + 12 = 0\) can be factorised as \((x + 3)(x + 4)\)
-
Therefore either \(x + 3 = 0\), or \(x + 4 = 0\)
Solving \(x + 3 = 0\) gives \(x = -3\), while solving \(x + 4 = 0\) gives \(x = -4\)
Therefore the two solutions are \(x = -3\) and \(x = -4\) -
Substituting these values back into the original equation gives \((-3)^2 + 7(-3) + 12 = 9 - 21 + 12 = 0\) and \((-4)^2 + 7(-4) + 12 = 16 - 28 + 12 = 0\) as required.
Once you have worked through the example above, have a go at using this technique to find the value of \(x\) in some or all of the following quadratic equations:
Factorising gives \((x + 6)(x + 1) = 0\)
Therefore \(x + 6 = 0\), or \(x + 1 = 0\)
Solving these equations respectively gives two solutions: \(x = -6\) or \(x = -1\)
Factorising gives \((x + 1)(x - 5) = 0\)
Therefore \(x + 1 = 0\), or \(x - 5 = 0\)
Solving these equations respectively gives two solutions: \(x = -1\) or \(x = 5\)
Factorising gives \(x(x + 3) = 0\)
Therefore \(x = 0\), or \(x + 3 = 0\)
Solving gives two solutions: \(x = 0\) or \(x = -3\)
Solving using the quadratic formula
Finally, a way that you can solve any quadratic equation is using the quadratic formula. Note that this will not always be the quickest way to solve it, so it is a good idea to have a quick check and assess whether the previous two techniques will work first, but it is a method that works in all situations - and is sometimes the only method you will be able to use.
The quadratic formula states that for a quadratic equation \(ax^2 + bx + c = 0\), the value of \(x\) is given by:
\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]Example: Solve the quadratic equation \(2x^2 + 3x - 10 = 0\)
Solution: Following the steps above, we have:
\[\begin{aligned} x &= \frac{-3 \pm \sqrt{3^2 - 4(2)(-10)}}{2(2)} \\\ &= \frac{-3 \pm \sqrt{9 + 80}}{4} \\\ &= \frac{-3 \pm \sqrt{89}}{4} \\\ &= \frac{-3 \pm 9.43}{4} \\\ &= \frac{6.43}{4} \textrm{ or } \frac{-12.43}{4} \\\ &= 1.61 \textrm{ or } -3.11 \end{aligned}\]Finally, substituting these values back into the original equation gives \(2(1.61)^2 + 3(1.61) - 10 \approx 0\) and \(2(-3.11)^2 + 3(-3.11) - 10 \approx 0\), as required.
Once you have worked through the example above, have a go at solving some or all of the following quadratic equations using one of the three techniques described above:
Factorising gives \((x + 2)^2 = 0\)
Therefore \(x + 2 = 0\)
Solving gives one solution: \(x = -2\)
Factorising gives \((x + 6)(x - 2) = 0\)
Therefore \(x + 6 = 0\) or \(x - 2 = 0\)
Solving these equations respectively gives two solutions: \(x = -6\) or \(x = 2\)
Factorising gives \((x + 13)(x - 4) = 0\)
Therefore \(x + 13 = 0\) or \(x - 4 = 0\)
Solving these equations respectively gives two solutions: \(x = -13\) or \(x = 4\)